Эллипсоиды можно разделить по назначению и по их ориентации относительно разных блоков блочной модели.
По назначению :
1. Эллипсоиды поиска.
2. Эллипсоиды анизотропии.
По ориентации в пространстве относительно блоков блочной модели :
1. Статические эллипсоиды.
2. Динамические эллипсоиды.
И эллипсоиды поиска и эллипсоиды анизотропии могут быть как статическими, так и динамическими.
Один и тот же эллипсоид может использоваться и как эллипсоид поиска и как эллипсоид анизотропии (но не всегда эллипсоид анизотропии, который может быть задан упрощенным образом, может использоваться в качестве эллипсоида поиска).
Назначение эллипсоида поиска - выбор исходных точек (проб) для расчета в конкретном блоке блочной модели.
Эллипсоид поиска помещается в точку центра базового блока, для которого ведется расчет (для субблока - в точку центра базового блока, к которому относится субблок) и производится поиск точек (точек середин интервалов из заданной таблицы БД разведочных выработок), попадающих внутрь эллипсоида.
Основные характеристики эллипсоида поиска:
- длины трех осей (задаются длины полуосей) эллипсоида;
- три угла поворота, определяющих ориентацию осей эллипсоида в пространстве;
- группа параметров, определяющих, достаточно ли внутри эллипсоида проб для расчета и помогающих отсечь часть проб в случае слишком большого количества проб внутри эллипсоида;
- группа параметров, позволяющих, при необходимости, производить расширение эллипсоида поиска в случае недостаточного количества проб для расчета.
Назначение эллипсоида анизотропии - вычисление анизотропного расстояния, используемого при расчете весовых коэффициентов для каждой из проб, участвующих в расчетах.
Основные характеристики эллипсоида анизотропии:
- соотношения длин осей эллипсоида главная ось / средняя ось и главная ось / малая ось (коэффициенты анизотропии). Для поддержания общего формата с эллипсоидами поиска в программе предусмотрен ввод длин трех осей, а коэффициенты анизотропии вычисляются в процессе расчетов.
- три угла поворота, определяющих ориентацию осей эллипсоида в пространстве;
Статический эллипсоид имеет одинаковую ориентацию в пространстве применительно ко всем блокам блочной модели, при обработке которых используется эллипсоид.
Ориентация в пространстве задается тремя углами поворота вокруг осей эллипсоида. Эти углы поворота задаются в рассматриваемом диалоге.
Динамические эллипсоиды имеют разную ориентацию в пространстве для разных блоков блочной модели.
Ориентация в пространстве задается тремя углами поворота, которые записываются в блоки блочной модели до начала использования динамических эллипсоидов в расчетах.
В программе имеются специальные механизмы для расчета и записи углов поворота динамических эллипсоидов.
На вкладке "Эллипсоиды" диалога "Построение блочной модели" задаются параметры эллипсоидов, необходимых для построения блочной модели.
Для каждого из наборов параметров (формируемых на вкладке "Наборы параметров") выбирается один из эллипсоидов, заданный на вкладке "Эллипсоиды".
Один и тот же эллипсоид может быть упомянут во многих наборах параметров.
Если для блочной модели еще не задан ни один эллипсоид, то большинство элементов диалога будут неактивными :
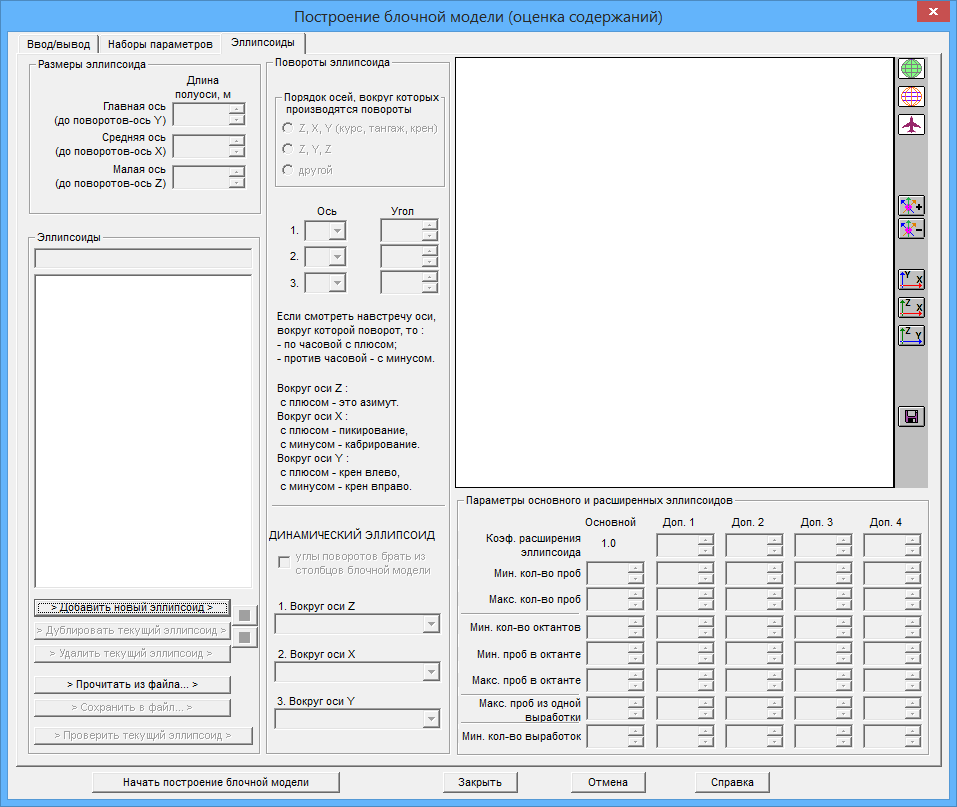
После нажатия на кнопку 
произойдет добавление в список нового эллипсоида с названием "Эллипсоид 1":
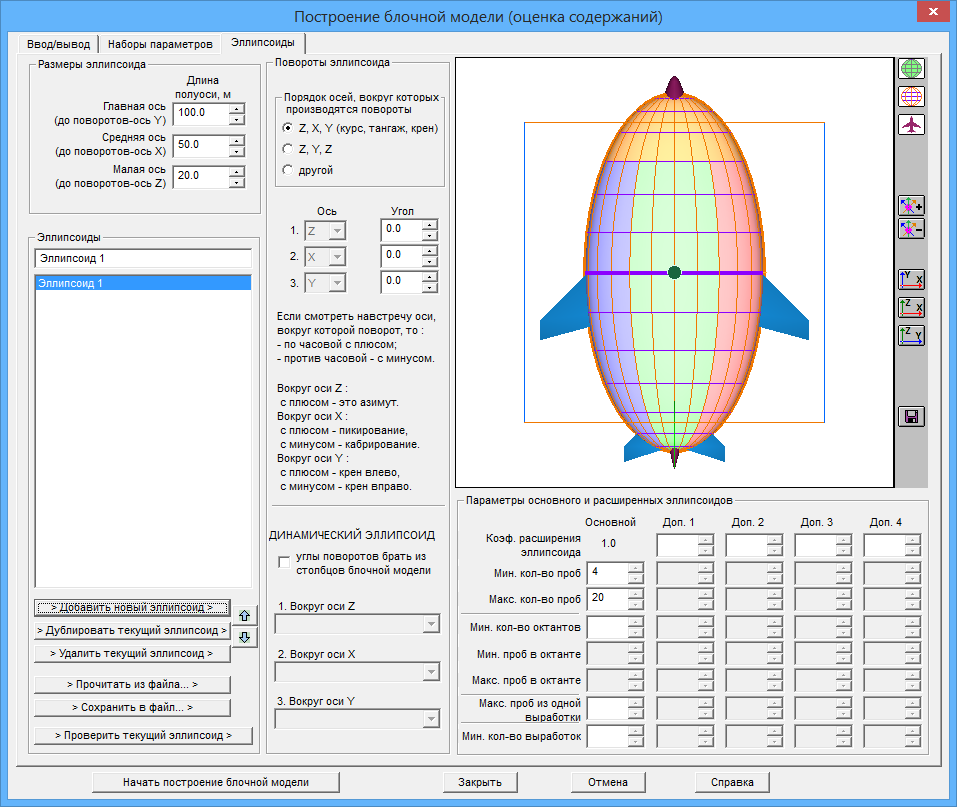
Размеры эллипсоида
Как правило, эллипсоид имеет разные размеры в разных направлениях.
Ось, вдоль которой эллипсоид имеет наибольший размер, называется главной осью, ось со средним размером называется средней осью, а третья ось - малой осью.
Задаются длины полуосей текущего эллипсоида (в метрах).
Если эллипсоид будет использоваться только как эллипсоид анизотропии, то абсолютные значения длин полуосей не имеют значения. Для эллипсоида анизотропии используются не абсолютные значения длин осей, а соотношения длин осей эллипсоида главная ось / средняя ось и главная ось / малая ось.
Эллипсоиды
Можно задавать много эллипсоидов. Для разных наборов параметров можно выбирать разные эллипсоиды.
Один из эллипсоидов в списке эллипсоидов является текущим (выделен в списке эллипсоидов). Параметры текущего эллипсоида и его графическое представление выводятся в элементах диалога.
Для работы со списком эллипсоидов предусмотрены следующие кнопки:
- добавление в список нового эллипсоида с названием "Эллипсоид N", где N - номер эллипсоида.
- добавление в список копии текущего эллипсоида с названием, повторяющим название текущего эллипсоида и добавлением в конце названия номера копии, т.к. названия эллипсоидов не могут быть одинаковыми.
- удаление текущего эллипсоида из списка.
- чтение из файла с расширением *.ble ранее записанных эллипсоидов. Прочитанные из файла эллипсоиды добавляются в конец списка. При совпадении названий программа добавляет в конце вставляемых названий соответствующее число, чтобы обеспечить уникальность названий эллипсоидов.
- запись в файл *.ble всех эллипсоидов из списка.
- переместить текущий эллипсоид вверх в списке.
- переместить текущий эллипсоид вниз в списке.
- производится проверка текущего эллипсоида.
Если в процессе проверки обнаруживается ошибка, то выводится сообщение об этом. Например :
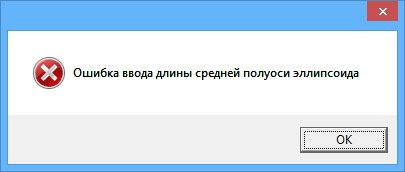
Можно либо продолжить проверку, чтобы программа сообщила обо всех ошибках для текущего эллипсоида (ответить "Да"), либо перейти к исправлению параметров (ответить "Нет").
Если в эллипсоидах, используемых для расчетов, будут ошибки, то при попытке начать построение модели программа сообщит, в каких эллипсоидах имеются ошибки и не начнет построение модели до тех пор, пока все ошибки не будут исправлены.
СТАРТОВОЕ ПОЛОЖЕНИЕ ЭЛЛИПСОИДА
Для того, чтобы задавать положение эллипсоида в пространстве при помощи углов поворота, необходимо определиться со стартовым положением эллипсоида.
В математике зачастую главная ось эллипсоида направлена вдоль оси X, средняя ось - вдоль оси Y, а малая ось - вдоль оси Z.
При построении блочных моделей чаще всего первым поворотом эллипсоида (главной оси эллипсоида) делается поворот вокруг оси Z, который удобнее всего задавать азимутом.
Азимут задается положительным углом, измеряемым по часовой стрелке от направления на север (от оси Y). Поэтому логично исходный, до поворотов, эллипсоид расположить так, чтобы главная ось была направлена на север (вдоль оси Y), средняя ось - вдоль оси X, малая ось - вдоль оси Z.
Повороты эллипсоида вокруг собственных осей
Порядок осей, вокруг которых производятся повороты
Для определения ориентации эллипсоида в пространстве задаются 3 последовательных поворота.
Первый поворот выполняется относительно исходного положения осей.
Второй поворот выполняется относительно нового положения осей эллипсоида, которое стало после первого поворота.
Третий поворот выполняется относительно нового положения осей эллипсоида, которое стало после второго поворота.
Большое значение имеет порядок, в котором берутся оси, вокруг которых производится поворот. Например, если произвести поворот вокруг оси Z, затем - вокруг оси X и, наконец, вокруг оси Y, то это не будет эквивалентно повороту (на те же углы для каждой из осей) сначала вокруг Z, затем - вокруг Y, затем - вокруг X.
ЗНАКИ УГЛОВ ПОВОРОТА
В математике чаще всего встречается, что углы поворота против часовой стрелки имеют знак "плюс", а углы поворота по часовой стрелке имеют знак "минус".
Так как при построении блочных моделей поворот вокруг оси Z чаще всего задается азимутом, то в DIGIMINE и для поворотов вокруг остальных осей принято что углы со знаком "плюс" используются для поворотов по часовой стрелке, то есть так как для азимута, а не так, как в обычно в математике.
Для определения направления поворота смотрим навстречу положительному направлению оси, вокруг которой производится поворот. Например, азимут измеряется, когда смотрим навстречу оси Z, т.е. сверху вниз.
ИСПОЛЬЗОВАНИЕ "САМОЛЕТНОЙ" ТЕРМИНОЛОГИИ
Несмотря на то, что для определения положения эллипсоида в пространстве используются всего три поворота, ошибки при задании углов поворота отнюдь не редкое явление.
Поэтому в DIGIMINE, для уменьшения возможных ошибок, предусмотрено визуальное представление эллипсоида в виде самолета с использованием соответствующей терминологии.
Фюзеляж самолета располагается вдоль главной оси эллипсоида, совпадающей с осью Y эллипсоида ("летим" вдоль направления наименьшей изменчивости, обычно по простиранию).
Крылья - вдоль средней оси, оси X. От левого крыла к правому идет положительное направление оси X.
Для малой оси эллипсоида остается ось Z.
Для самолета поворот вокруг оси Z обычно называется курсом, задается азимутом, выражаемым положительным числом. Но разрешается ввод и отрицательного числа, например, вместо азимута 350 градусов допускается ввод угла (-10) градусов.
Поворот вокруг оси X называется тангажом (вниз - пикирование, вверх - кабрирование). С плюсом - пикирование, с минусом - кабрирование.
Поворот вокруг оси Y называется креном. С плюсом - крен влево, с минусом - крен вправо.
В диалоге предусмотрены 2 фиксированных, наиболее часто употребляемых, порядка осей, вокруг которых производятся повороты, а также имеется возможность задать произвольный порядок осей.
Z, X, Y (курс, тангаж, крен) - часто используемый порядок осей, вокруг которых производятся повороты.
Удобен, в частности, тем, что после первого поворота азимут направления главной оси уже не изменяется.
Такой порядок осей (Z, X, Y), вокруг которых производятся повороты, всегда используется для динамических эллипсоидов.
Z, Y, Z - после первого поворота "самолет" оказывается ориентирован вдоль простирания рудного тела, после второго поворота "самолет" оказывается в плоскости рудного тела (но фюзеляж пока еще горизонтален), а третий поворот, опять вокруг оси Z (но уже новой оси Z), учитывает склонение.
Другой - порядок осей задается пользователем.
Управляющий элемент с графическим изображением эллипсоида
Предусмотрены следующие виды представления эллипсоида и самолета, соответствующего ему:
1. Эллипсоид в виде набора моделей поверхностей ( 
):
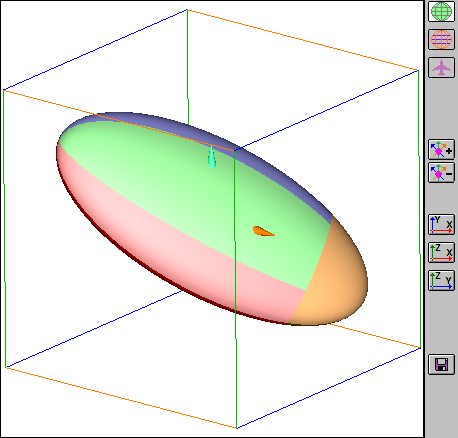
Эллипсоид состоит из восьми разноцветных незамкнутых моделей поверхностей, вместе образующих замкнутый эллипсоид.
"Верхняя" и "нижняя" части эллипсоида состоят каждая из четырех моделей поверхностей одинакового цвета, но разной интенсивности цвета.
"Нижние" модели поверхностей имеют более насыщенный цвет.
Зеленая модель поверхности простирается в направлении главной оси эллипсоида.
Оранжевая модель поверхности направлена в сторону положительного направления главной оси эллипсоида (играет роль стрелки на главной оси).
Синяя и красная модели поверхности располагаются слева и справа от зеленой.
2. Эллипсоид в виде полилиний "меридианов" и "параллелей" ( 
):
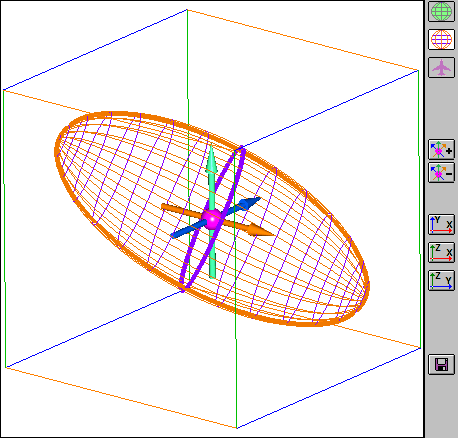
Линии "меридианов" - оранжевого цвета, линии "параллелей" - фиолетового цвета.
"Экватор" показан толстой полилинией фиолетового цвета. Если провести прямую линию между "полюсами", то получим главную ось эллипсоида.
3. Самолет, показывающий положение эллипсоида в пространстве ( 
) :
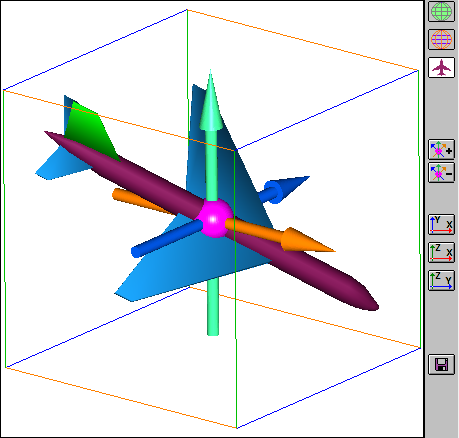
Фюзеляж самолета располагается вдоль главной оси эллипсоида, совпадающей с осью Y эллипсоида.
Крылья - вдоль средней оси, оси X. От левого крыла к правому идет положительное направление оси X.
Малая ось направлена "вверх" от плоскости самолета.
Рассмотренные графические представления эллипсоида могут быть включены/выключены при помощи соответствующих элементов в графическом меню - , , .
Если включить все графические представления эллипсоида, то получим:
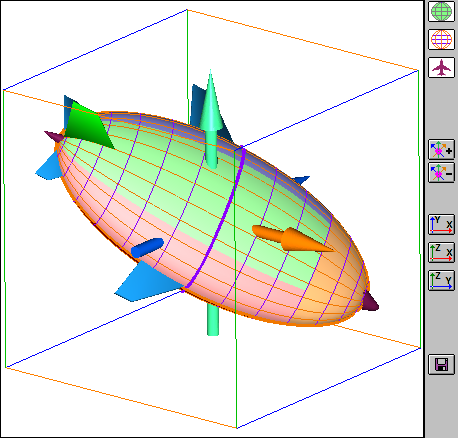
В графическом элементе диалога изображаются также объемные стрелки и шар.
Синяя стрелка показывает направление на север, оранжевая - направление на восток, а зеленая - направление вверх.
Размеры стрелок можно изменять при помощи элементов графического меню - 
и 
.
Кроме, того линиями разного цвета изображается каркас-куб, размером чуть меньше удвоенной длины главной полуоси.
Синие линии этого каркаса показывают направление юг-север, оранжевые линии показывают направление запад-восток, а зеленые линии - направление низ-верх.
По положению эллипсоида относительно объемных стрелок и линий каркаса-куба можно судить об ориентации эллипсоида в пространстве.
Элементы 
, 
и 
служат для того, чтобы задать в окне виды, параллельные оссям XY, XZ и YZ.
Если изображение эллипсоида было смещено относительно центра окна, то нажатие на любую из этих трех кнопок приводить к перемещению эллипсоида в центр окна.
При помощи кнопки 
производится вызов диалога "Формирование файлов для текущего эллипсоида" для формирования и записи в проект файлов, описывающих графические представления эллипсоида.
Кроме записи эллипсоида в файл и последующего просмотра информации из этого файла, в DIGIMINE имеется еще одна возможность визуализации эллипсоидов.
При настройке параметров отрисовки блочной модели в окне можно задать, чтобы для текущего (активного в таблице блочной модели) блока рисовался заданный эллипсоид.
ДИНАМИЧЕСКИЙ ЭЛЛИПСОИД
Если отмечено углы поворотов брать из столбцов блочной модели, то задаются 3 столбца блочной модели, в которых записаны углы поворотов для каждого из блоков.
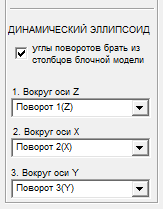
Перед началом расчетов для каждого блока блочной модели производится настройка положения осей эллипсоида в соответствии со значениями углов поворота, записанных для блока.
Подробнее о расчете и записи углов поворота в блочную модель см. :
Исходные эллипсоиды для динамических эллипсоидов
Заполнение блочной модели углами поворота
Пример построения моделей поверхностей для динамических эллипсоидов
Пример расчета ориентации динамических эллипсоидов
Параметры основного и расширенных эллипсоидов
Расширенные эллипсоиды имеют ту же ориентацию и те же пропорции между длинами полуосей, что и основной эллипсоид, но размеры умножаются на некоторый коэффициент. Возможно также использование расширенного эллипсоида с теми же размерами, но более мягкими требованиями к количеству проб для расчета.
Основное, но не единственное, назначение расширенных эллипсоидов связано с категоризацией запасов. Если в каком-либо эллипсоиде не набирается достаточного для расчетов количества проб и имеется расширенный эллипсоид, то программа делает попытку произвести поиск проб в расширенном эллипсоиде.
Информацию о том, какой эллипсоид использовался при расчете того или иного блока, можно получить, если задать запись в блочную модель номера эллипсоида.
Основной эллипсоид будет иметь номер 0, а расширенные эллипсоиды могут иметь номера от 1 до 5.
Параметры, определяющие количество проб, используемых при расчетах.
Минимальное кол-во проб - обязательный параметр.
Максимальное кол-во проб - обязательный параметр.
Минимальное кол-во октантов - необязательный параметр.
Мин. кол-во проб в октанте - необязательный параметр.
Макс. кол-во проб в октанте - необязательный параметр.
Макс. проб из одной выработки - необязательный параметр.
Мин. кол-во выработок - необязательный параметр.
Комментарий к тому, как используются параметры, определяющие количество проб, используемых при расчетах
А. Сначала выбираются все пробы, попадающие внутрь эллипсоида, с учетом принадлежности к домену, если задана.
Б. Если общее количество проб меньше, чем Минимальное кол-во проб, то считается, что проб в эллипсоиде недостаточно, расчет не производится.
Если имеется эллипсоид большего размера (расширенный эллипсоид), то делается попытка набрать необходимое количество проб в расширенном эллипсоиде.
В. Далее рассмотрим сначала случай без использования октантов (Минимальное кол-во октантов равно нулю или пустому значению).
В1. Если задано ограничение по количеству проб из каждой выработки (Макс. проб из одной выработки), то для выработок с большим количеством проб, попавших в эллипсоид, производится удаление наиболее далеких проб.
В2. Если оставшееся общее количество проб окажется меньше, чем чем Минимальное кол-во проб, либо количество выработок меньше, чем Мин. кол-во выработок, то в текущем эллипсоиде расчет не производится.
В3. Если общее количество проб больше, чем Максимальное кол-во проб, то наиболее далекие пробы исключаются.
Если после исключения наиболее далеких проб получилось, что количество выработок стало меньше, чем Мин. кол-во выработок, то производится последовательное возвращение наиболее близких из из исключенных проб до тех пор, пока количество выработок не станет равным Мин. кол-во выработок (в таком случае общее количество проб станет больше, чем Максимальное кол-во проб).
Г. Случай с использованием октантов (Минимальное кол-во октантов больше нуля, т.е. октанты используются).
Г1. Если задано ограничение по количеству проб из каждой выработки (Макс. проб из одной выработки), то для выработок с большим количеством проб, попавших в ОКТАНТ эллипсоида, производится удаление наиболее далеких проб.
Максимальное количество проб из одной выработки, в данном случае, относится не ко всему эллипсоиду, а к каждому из октантов эллипсоида!.
Г2. Если оставшееся общее количество проб меньше, чем чем Минимальное кол-во проб, либо количество выработок меньше, чем Мин. кол-во выработок, то в текущем эллипсоиде расчет не производится.
Г3. Считается количество заполненных октантов, т.е. октантов, имеющих не менее Мин. кол-во проб в октанте. Если количество заполненных октантов меньше Минимальное кол-во октантов, то считается, что проб в эллипсоиде недостаточно и расчет текущем эллипсоиде не производится.
Г4. Если количество проб в октанте больше Макс. кол-во проб в октанте, то удаляются наиболее далекие пробы этого октанта.
Г5. Если общее количество проб в эллипсоиде больше, чем Максимальное кол-во проб, то производится исключение "далеких" проб. Но при этом в каждом октанте оставляется не менее Мин. кол-во проб в октанте (даже если остаются "далекие"). Если после исключения наиболее далеких проб получилось, что количество выработок стало меньше, чем Мин. кол-во выработок, то производится последовательное возвращение наиболее близких из из исключенных проб до тех пор, пока количество выработок не станет равным Мин. кол-во выработок (в таком случае общее количество проб станет больше, чем Максимальное кол-во проб).
Для понимания того, как используются эти параметры, рассмотрим сначала случай без использования октантов (Минимальное кол-во октантов равно нулю или пустому значению).
Сначала ищутся все пробы, попадающие в эллипсоид (с учетом Доп. условия (формула) для выбора интервалов из таблицы БД, если задано).
Если задано Макс. проб из одной выработки, то из тех проб, которые попали в эллипсоид, убираются "лишние" пробы, относящиеся к одной и той же выработке. Оставляются не более заданного количества ближайших (с учетом анизотропии) проб из каждой выработки.
Если оставшееся количество проб превышает значение Максимальное кол-во проб, то наиболее далекие (здесь и ниже - с учетом анизотропии, заданной эллипсоидом поиска) пробы убираются.
Если оставшееся количество проб меньше значения Минимальное кол-во проб, то расчет не выполняется - производится попытка взять очередной расширенный эллипсоид, а если его нет, то производится переход к следующей точке в блочной модели.
Использование параметров при наличии дополнительных условий, связанных с количеством проб в разных октантах эллипсоида.
Октант - это 1/8 часть эллипсоида. Эллипсоид разделяется плоскостями, параллельными его осям XY, XZ и YZ. В результате получается 8 равных частей.
Сначала ищутся все пробы, попадающие в эллипсоид (с учетом Доп. условия (формула) для выбора интервалов из таблицы БД, если задано).
Если задано Макс. проб из одной выработки, то из тех проб, которые попали в каждый октант эллипсоида (но не в эллипсоид в целом), убираются "лишние" пробы, относящиеся к одной и той же выработке. Оставляются не более заданного количества ближайших (с учетом анизотропии) проб из каждой выработки.
Если после этого количество заполненных (содержащих не менее Мин. кол-во проб в октанте ) октантов меньше Минимальное кол-во октантов, то расчет не выполняется, берется следующий расширенный эллипсоид, а если его нет, то производится переход к следующей точке в блочной модели.
Если оставшееся количество проб в каком-либо октанте превышает Макс. кол-во проб в октанте, то наиболее далекие пробы из таких октантов убираются.
Если оставшееся общее количество проб меньше значения Минимальное кол-во проб, то расчет не выполняется - производится попытка взять очередной расширенный эллипсоид, а если его нет, то производится переход к следующей точке в блочной модели.
Если общее количество оставшихся проб больше, чем Максимальное кол-во проб, то производится убирание "далеких" проб. В каждом октанте оставляется не менее Мин. кол-во проб в октанте проб (даже если остаются "далекие"). Если после этого осталось более, чем Максимальное кол-во проб проб, то все они используются для расчета.