Метод обратных расстояний в степени является одним из видов линейных интерполяторов.
В западных программах для этого метода используется термин Inverse Power of Distance (IPD).
Также можно встретить термины Inverse Distance to a Power и Inverse Distance Weighting (IDW).
Формула для расчета значения в некоторой точке пространства (например, в точке, находящейся в центре какого-либо блока блочной модели):
,
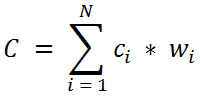где
С - оцениваемое значение (содержания) в некоторой точке пространства;
N - количество точек с известными значениями (содержаний), используемых при расчетах для одной оцениваемой точки;
ci - известное значение (содержания) в i-той точке;
wi - весовой коэффициент для значения в i-той точке.
Весовые коэффициенты для каждой исходной точки вычисляются по формуле:
,
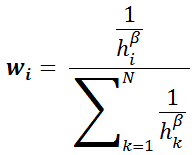где
hi - "расстояние" от точки, в которой оценивается значение (содержания) до i-той точки с известным значением.
,
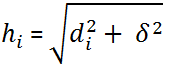где
di - расстояние, с учетом анизотропии, от точки, в которой оценивается значение (содержания) до i-той точки с известным значением.
,
где
dx, dy, dz - смещения (метров) по осям i-той точки от точки, для которой производится оценка (в системе координат повернутого соответствующим образом эллипсоида).
Центр эллипсоида - в точке, для которой производится оценка.
Ось Y совпадает с главной полуосью, ось X - со средней полуосью, а осью Z - с малой полуосью эллипсоида.
kx - коэффициент, показывающий во сколько раз длина главной полуоси больше длины средней полуоси эллипсоида;
kz - коэффициент, показывающий во сколько раз длина главной полуоси больше длины малой полуоси эллипсоида.
Так как главная полуось совпадает с осью Y, то коэффициент при dy опускается (всегда равен 1.0).
δ - сглаживающий параметр. Если этот параметр больше нуля, то для исходных значений, расположенных очень близко к точке, в которой производится оценка, снижается весовой коэффициент.
Если сглаживающий параметр задается равным нулю, то при наличии близкорасположенной точки весовые коэффициенты для остальных точек стремятся к нулю, даже если они попадают непосредственно в оцениваемый блок блочной модели.
Ориентировочно можно считать, что этот параметр задается в метрах.
Заметим, что использование при расчетах точек дискретизации снимает проблему близкорасположенных точек, т.к. конкретная исходная точка может оказаться очень близко лишь к одной точке дискретизации.
β - степень для "расстояния". Чаще всего используется значение, равное 2 (в таком случае нередко используется название "метод обратных квадратов").
Знаменатель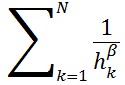 
служит для того, чтобы сумма весовых коэффициентов Wi равнялась единице.
При расчетах для каждой i-той исходной точки сначала вычисляются значения (назовем их предварительными весами):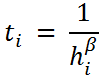 
Затем находится сумма предварительных весов :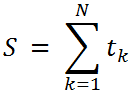 
Окончательные весовые коэффициенты :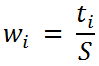 
Для иллюстрации расчетов по приведенным формулам, а также влияния параметра сглаживания рассмотрим пример вычисления содержания в оцениваемой точке для 4-х исходных проб (N=4).
В столбцах таблиц записано:
i - номер точки, принимающей участие в расчете.
dx, dy, dz - смещения (метров) по осям i-той точки от точки, для которой производится оценка (в системе координат повернутого соответствующим образом эллипсоида).
di - "расстояние" с учетом анизотропии.
hi - "расстояние" с учетом параметра сглаживания.
ti - предварительный вес. S - сумма предварительных весов.
wi - окончательный весовой коэффициент. Сумма весовых коэффициентов W всегда равна 1.0.
ci - исходные содержания в пробах.
ci*wi - столбец для вычисления итогового содержания в оцениваемой точке. Сумма по столбцу дает искомый результат.
Степень β = 2.0
1. kx = 1.0 kz = 1.0 (Эллипсоид в виде сферы) δ = 0.0
i |
dx |
dy |
dz |
di |
hi |
ti |
wi |
ci |
ci*wi |
1 |
0.3 |
0.0 |
0.0 |
0.3 |
0.3 |
11.111 |
0.995 |
1.0 |
0.995 |
2 |
0.0 |
5.0 |
0.0 |
5.0 |
5.0 |
0.040 |
0.004 |
4.0 |
0.014 |
3 |
0.0 |
0.0 |
-10.0 |
10.0 |
10.0 |
0.010 |
0.001 |
5.0 |
0.004 |
4 |
-10.0 |
5.0 |
10.0 |
15.0 |
15.0 |
0.004 |
0.0004 |
5.0 |
0.002 |
|
|
|
|
|
|
S = 11.166 |
W = 1.000 |
|
C = 1.016 |
2. kx = 1.0 kz = 1.0 (Эллипсоид в виде сферы) δ = 1.0
i |
dx |
dy |
dz |
di |
hi |
ti |
wi |
ci |
ci*wi |
1 |
0.3 |
0.0 |
0.0 |
0.3 |
1.044 |
0.917 |
0.945 |
1.0 |
0.946 |
2 |
0.0 |
5.0 |
0.0 |
5.0 |
5.099 |
0.038 |
0.040 |
4.0 |
0.159 |
3 |
0.0 |
0.0 |
-10.0 |
10.0 |
10.050 |
0.010 |
0.010 |
5.0 |
0.051 |
4 |
-10.0 |
5.0 |
10.0 |
15.0 |
15.033 |
0.004 |
0.005 |
5.0 |
0.023 |
|
|
|
|
|
|
S = 0.970 |
W = 1.000 |
|
C = 1.178 |
3. kx = 2.0 kz = 4.0 δ = 1.0
i |
dx |
dy |
dz |
di |
hi |
ti |
wi |
ci |
ci*wi |
1 |
0.3 |
0.0 |
0.0 |
0.6 |
1.166 |
0.735 |
0.949 |
1.0 |
0.949 |
2 |
0.0 |
5.0 |
0.0 |
5.0 |
5.099 |
0.038 |
0.050 |
4.0 |
0.199 |
3 |
0.0 |
0.0 |
-10.0 |
40.0 |
40.012 |
0.001 |
0.001 |
5.0 |
0.004 |
4 |
-10.0 |
5.0 |
10.0 |
45.0 |
45.011 |
0.000 |
0.0006 |
5.0 |
0.003 |
|
|
|
|
|
|
S = 0.775 |
W = 1.000 |
|
C = 1.155 |
Отметим, что при использовании сглаживающего параметра δ > 0.0 для проб с малым (сопоставимым с δ) значением di существенно изменяется hi (сравним таблицы 1 и 2). В результате происходит уменьшение весовых коэффициентов для таких проб.
Для проб с относительно большим значением di изменение hi из-за использования сглаживающего параметра незначительно.