Исходной информацией для расчетов являются модели поверхностей, использованные в примере построения поверхностей для динамических эллипсоидов.
Каркас рудного тела:
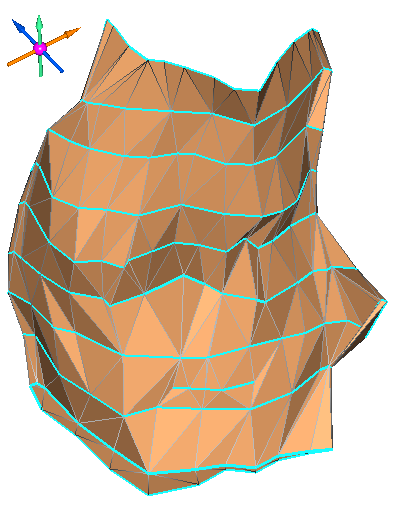
Исходные модели поверхностей для вычисления ориентации динамических эллипсоидов:
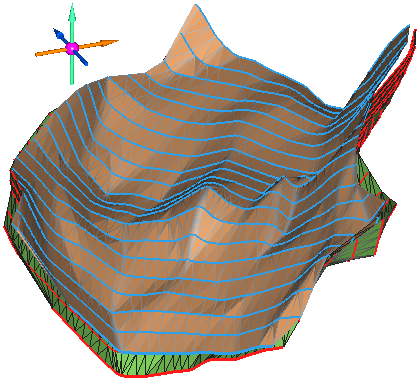
Перед вычислением и записью углов поворота для динамических эллипсоидов необходимо иметь блочную модель с блоками, в которые будет производиться запись.
Для создания новой блочной модели выберем пункт главного меню "Файл / Новый файл..." или нажмем на кнопку 
в графическом меню окна проекта.
Далее выбираем, что создается файл блочной модели, после чего появляется диалог :
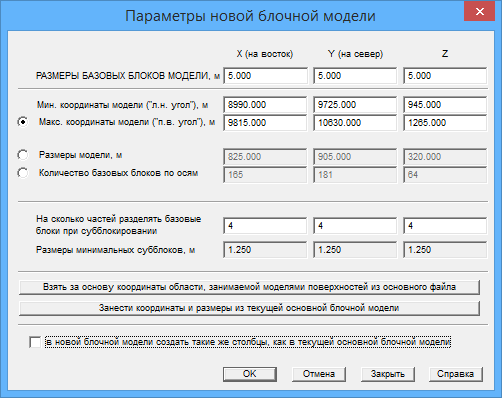
Задаем параметры блоков и субблоков и предельные координаты блочной модели по каждой из координатных осей.
Для того, чтобы программа сама вычислила предельные координаты, необходимо перед созданием блочной модели загрузить в проект файл с каркасом рудного тела и сделать этот файл основным.
Тогда для получения предельных координат блочной модели достаточно нажать в диалоге кнопку Взять за основу координаты области, занимаемой моделями поверхностей из основного файла.
После создания новой пустой блочной модели произведем заполнение ее блоками / субблоками, попадающими в каркас рудного тела.
Файл с каркасом рудного тела должен быть загружен в проект и сделан основным файлом.
Нажимаем на кнопку 
в графическом меню окна с таблицей блочной модели.
В появившемся диалоге отмечаем создавать новые блоки / субблоки внутри каркасов и ставим галочку в столбце Для расчетов в таблице с моделями поверхностей:
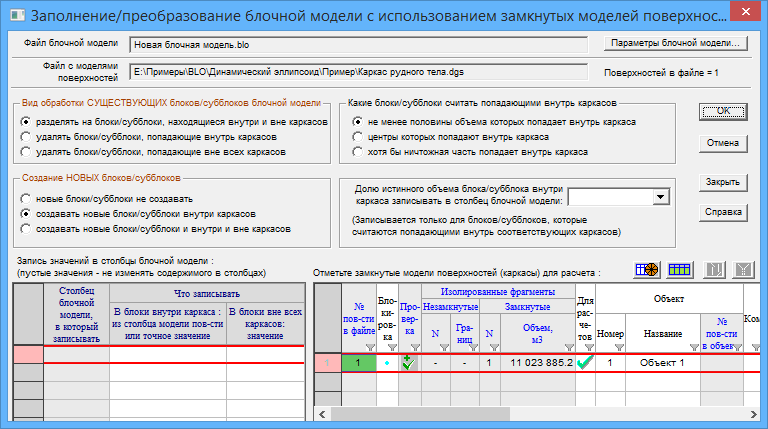
После соответствующей обработки будет создана блочная модель со следующими параметрами:
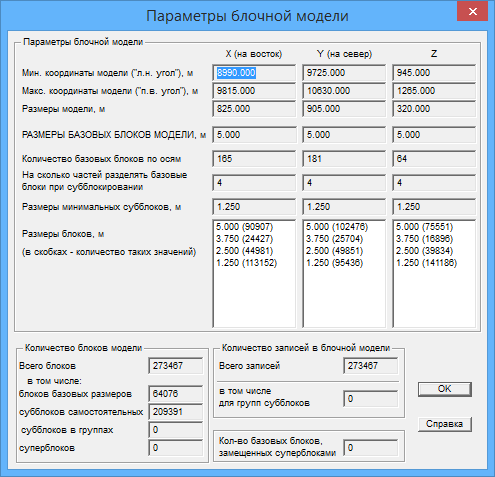
Приступим собственно к расчету ориентации динамических эллипсоидов.
Нажимаем на кнопку 
в графическом меню окна с таблицей блочной модели для вызова диалога "Вычисление и запись углов поворота динамических эллипсоидов" :
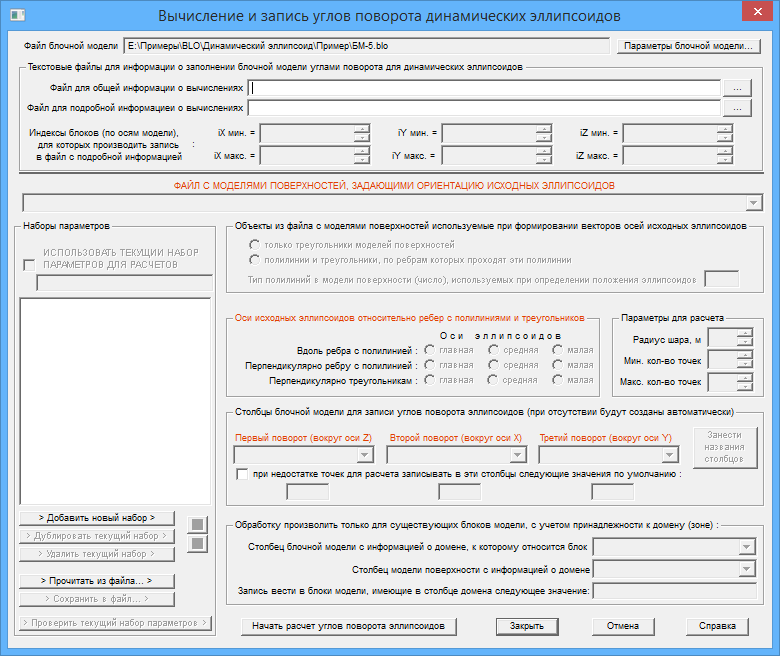
Далее произведем два варианта расчета углов поворота динамических эллипсоидов, используя для каждого из вариантов один и тот же исходный файл с моделями поверхностей :
Вариант 1. Исходные эллипсоиды формируются из полилиний в моделях поверхностей и треугольников, по ребрам которых проходят эти полилинии.
Вариант 2. Исходные эллипсоиды формируются с использованием только треугольников в моделях поверхностей.
Для каждого из вариантов сформируем свой набор параметров и свой набор столбцов для записи углов поворота динамических эллипсоидов.
Настройка параметров для варианта 1
Нажимаем кнопку > Добавить новый набор >, а затем задаем следующие параметры:
- Название набора параметров - "ВАРИАНТ 1 (с полилиниями)".
- Из загруженных в проект файлов выбираем файл с исходными моделями поверхностей, которые определяют положение в пространстве и ориентацию исходных эллипсоидов.
- Задаем, что из файла с моделями поверхностей использовать полилинии и треугольники, по ребрам которых проходят полилинии.
- Тип полилинии не задаем, что означает использование полилиний любых типов.
- Задаем, что главная ось исходных эллипсоидов располагается перпендикулярно ребрам с полилиниями и в плоскости, получаемой в результате усреднения плоскостей двух треугольников, в которые входит это ребро;
средняя ось - совпадает с ребром, по которому проходит полилиния; малая ось - перпендикулярно двум другим осям.
- Задаем параметры для расчета с использованием метода обратных квадратов (обратно пропорционально квадрату расстояния) - радиус шара поиска, минимальное и максимальное количество точек для расчета.
- Задаем названия столбцов в блочной модели, в которые записывать углы поворота для каждого блока блочной модели.
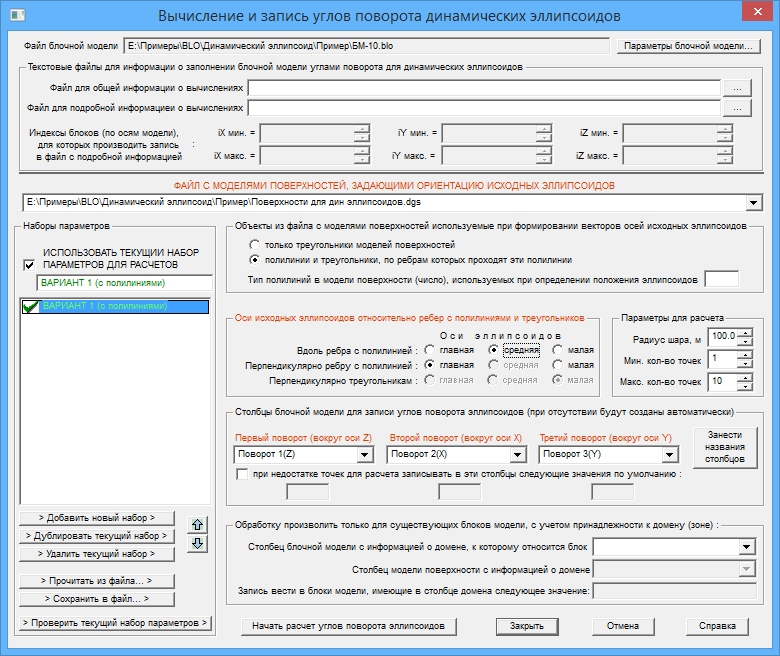
Настройка параметров для варианта 2
Нажимаем кнопку > Добавить новый набор >, а затем задаем следующие параметры:
- Название набора параметров - "ВАРИАНТ 2 (только треугольники)".
- Из загруженных в проект файлов выбираем тот же файл с исходными моделями поверхностей, которые определяют положение в пространстве и ориентацию исходных эллипсоидов.
- Задаем, что из файла с моделями поверхностей использовать только треугольники.
- Задаем, что главная ось исходных эллипсоидов располагается по простиранию плоскости треугольника; средняя ось - по линии падения плоскости треугольника; малая ось - перпендикулярно двум другим осям.
- Задаем параметры для расчета с использованием метода обратных квадратов (обратно пропорционально квадрату расстояния) - радиус шара поиска, минимальное и максимальное количество точек для расчета.
- Задаем названия столбцов в блочной модели, в которые записывать углы поворота для каждого блока блочной модели.
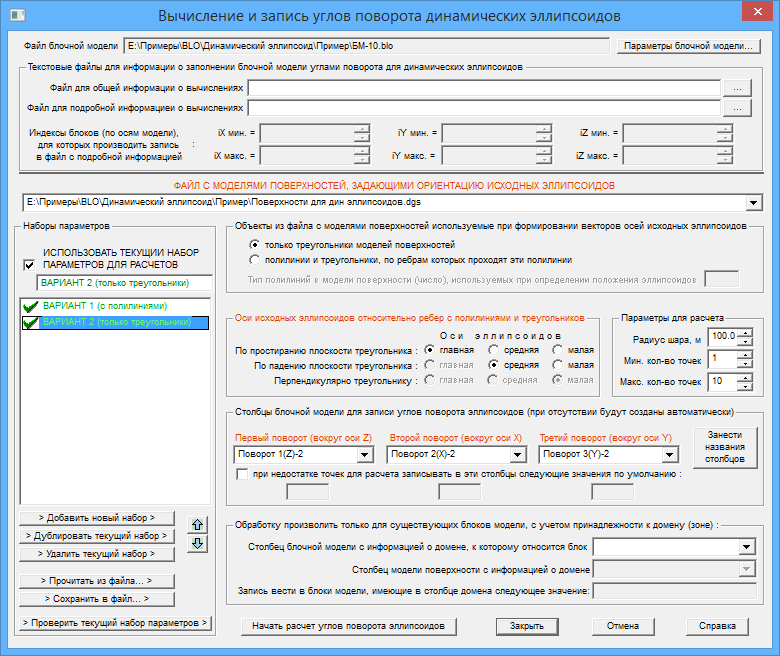
После нажатия кнопки Начать расчет углов поворота эллипсоидов будут выполнены сначала расчеты по ВАРИАНТУ 1, а затем по ВАРИАНТУ 2.
В результате выполнения расчетов в таблице блочной модели будут созданы шесть столбцов, в которых будут записаны углы поворота. Три столбца - для первого варианта динамических эллипсоидов и еще три столбца - для второго варианта динамических эллипсоидов:
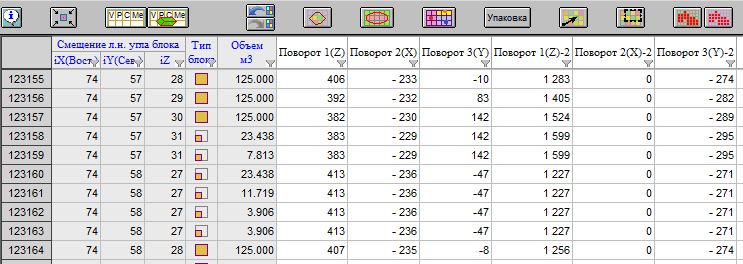
Углы поворота рассчитываются для точек центров базовых блоков блочной модели.
Для всех субблоков, относящихся к одному и тому же базовому блоку будут записаны одинаковые значения углов поворота. В примере на приведенном выше рисунке - это 2 субблока, относящихся к базовому блоку с индексами iX=74/iY=57/iZ=31 и 4 субблока, относящихся к базовому блоку с индексами iX=74/iY=58/iZ=27.
Значения углов поворота записываются целыми числами в десятых долях градуса. То есть, число 406 означает, что угол поворота равен 40.6 градусов.
В DIGIMINE предусмотрена визуализация ориентации динамических эллипсоидов в каждом блоке блочной модели при помощи специальных значков, состоящих из пары треугольников.
Треугольники значка показывают направления осей эллипсоида:
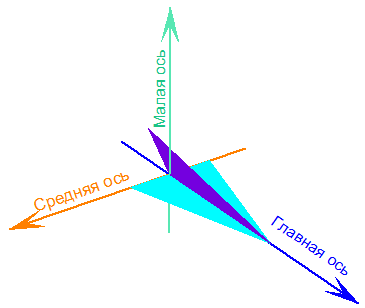
На расположенных ниже рисунках отрисованы значки, показывающие направления осей динамических эллипсоидов для каждого блока блочной модели.
Отрисовка самих блоков блочной модели выключена.
Значки динамических эллипсоидов отрисованы вместе с моделями поверхностей, использованными для расчета динамических эллипсоидов. Это позволяет видеть только "верхний слой" значков эллипсоидов, находящихся "над" моделью поверхности и удобнее для визуального восприятия.
Ориентация динамических эллипсоидов, полученных при расчетах по ВАРИАНТУ 1 (с полилиниями) :
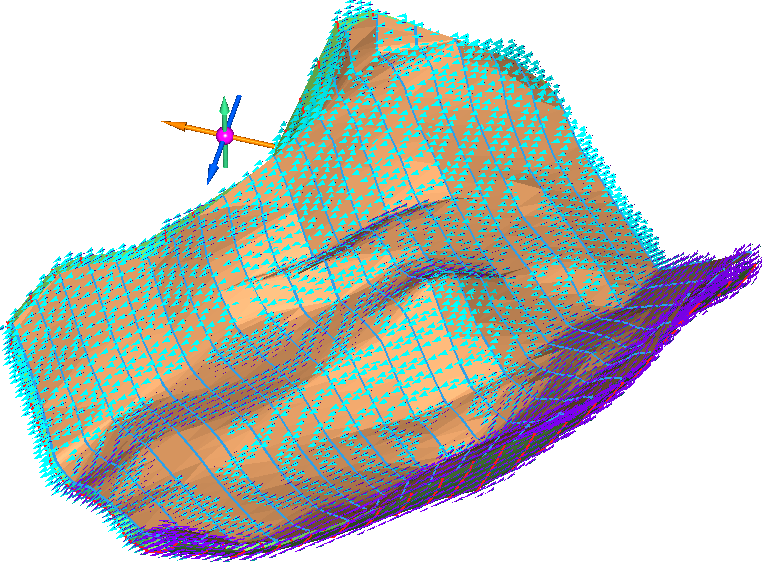
Ориентация динамических эллипсоидов, полученных при расчетах по ВАРИАНТУ 2 (только треугольники) :
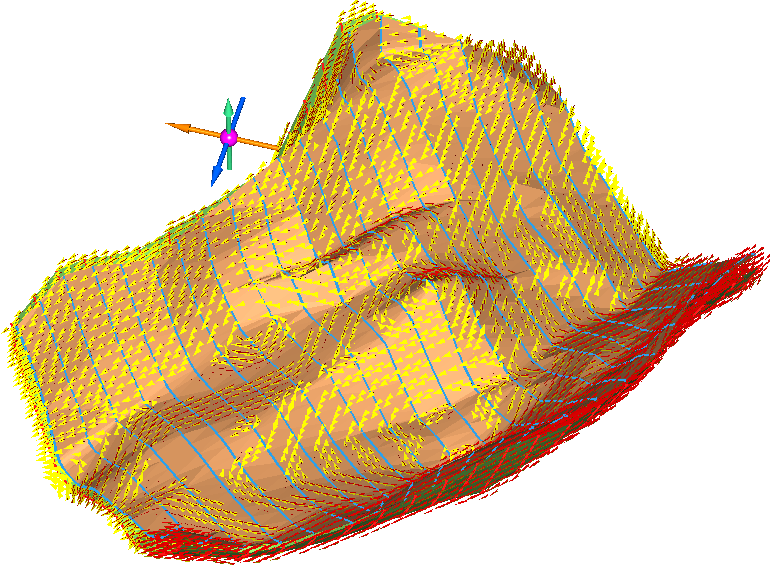
Отметим, что по ВАРИАНТУ 2 в местах локальных "вершин" и "впадин" значки эллипсоидов стремятся ориентироваться по кругу. Это вполне логично, так как склоны горы относительно вершины горы направлены в разные стороны по кругу, а этот вариант использования треугольников предполагает получение только азимута и угла падения плоскостей (имея только плоскости треугольников большего не получить).
А по ВАРИАНТУ 1 значки глобально располагаются в одном направлении.
Одновременная отрисовка значков эллипсоидов по обоим вариантам в том месте, где направления эллипсоидов по разным вариантам существенно различаются:
Кроме того, обратим внимание на ориентацию эллипсоидов, если смотреть в том направлении, как на продольном разрезе.
Главная ось эллипсоидов по ВАРИАНТУ 1 ориентирована в соответствии со склонением рудного тела:
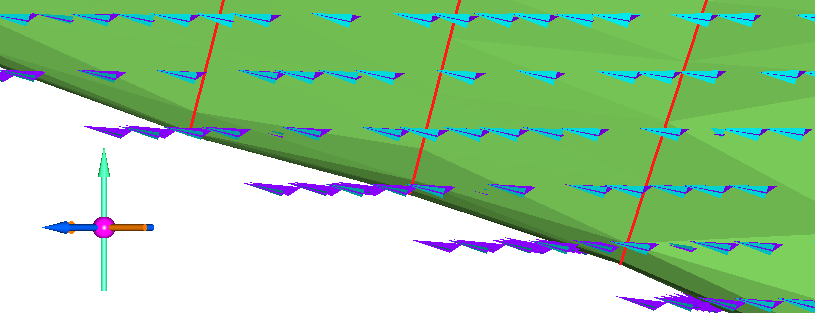
Главная ось эллипсоидов по ВАРИАНТУ 2 всегда расположена горизонтально :
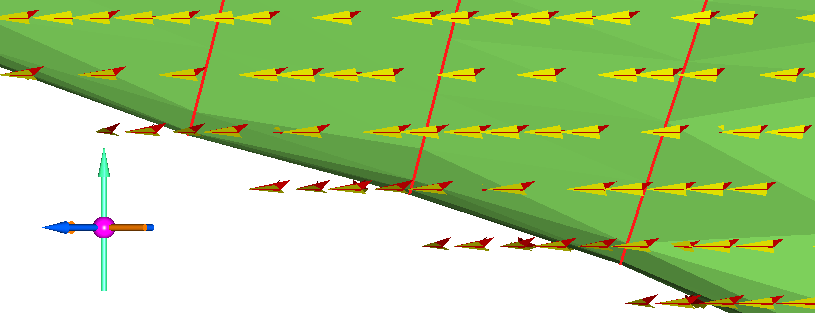
Если при получении точек и ориентации исходных эллипсоидов используются только треугольники моделей поверхностей, то одна из осей всех динамических эллипсоидов (обычно главная или средняя) будет горизонтальной.
Если исходными данными будут только азимуты и углы падения, задаваемые в некоторых программах при помощи полилиний, то одна из осей всех динамических эллипсоидов также будет горизонтальной.