Одной из часто встречаемых задач при формировании рудных тел для подсчета запасов является вычисление истинной мощности пересечений рудных тел разведочными выработками.
Эта задача усложняется в тех случаях, когда рудное тело не имеет четких границ. Т.е. прежде чем вести речь о мощности рудного пересечения сначала нужно определить, а является ли пересечение рудным или безрудным. Тем более, что нередко требуется отстроить несколько вариантов рудных тел - для разных кондиционных параметров.
В программе DIGIMINE предусмотрена возможность в процессе расчета рудных интервалов по заданным кондициям приводить к истинной мощности каждый исходный интервал опробования, что не допускает формирования таких рудных интервалов, которые в итоге не дадут требуемой мощности, хоть и имеют немалую протяженность вдоль разведочной выработки.
Для этой цели при расчете рудных интервалов задается столбец с коэффициентом пересчета на истинную мощность, вычисленным для каждого исходного интервала опробования.
Возникает вопрос, как эффективнее вычислить коэффициенты пересчета на истинную мощность для каждого исходного интервала опробования ?
Рассмотрим один из способов, который можно использовать в программе DIGIMINE.
Суть его сводится к следующему:
1. Создается вспомогательная таблица, в которой по каждой скважине (или разведочной выработке другого типа) вводятся [достаточно длинные] интервалы, которые будут описывать части месторождения, пересекаемые выработкой, с различными параметрами залегания рудных тел.
В этой вспомогательной таблице создаются два редактируемых столбца - в один из них заносится азимут ПАДЕНИЯ рудных тел, во второй - угол падения.
Учитывая, что по каждой разведочной выработки будет всего лишь несколько таких интервалов, задача заполнения такой таблицы требует вполне приемлемых трудозатрат.
На начальной стадии, когда рудные тела еще не сформированы, параметры залегания рудных тел определяются приблизительно. В последующем, возможно, потребуется их корректировка. Хотя можно заметить, что небольшие погрешности в определении этих параметров не оказывают значимого влияния на конечный результат.
2. В таблице с исходным опробованием, из которой будут браться интервалы для расчета рудных интервалов (рудных пересечений), создаются два аналогичных, но уже расчетных, столбца, в которые, при помощи использования в расчетной формуле функции ДР_ТАБЛ_СРЕДНЕВЗВЕШЕННОЕ программой вычисляются и записываются азимут падения и угол падения рудных тел применительно к каждому исходному интервалу.
3. В таблице с исходным опробованием создается еще один расчетный столбец, в расчетной формуле которого используется функция МОЩНОСТЬ_ИСТИННАЯ_КОЭФФ.
В качестве параметров этой функции передаются упомянутые выше два столбца с азимутом и углом падения рудных тел.
Азимут и угол падения каждого интервала программа определяет самостоятельно.
Расчет производится по формуле П.М.Леонтовского (из формулы убрано умножение на длину интервала, т.к. в данном случае нас интересует коэффициент приведения интервала к истинной мощности, а не сама истинная мощность):
K = sin(A) *cos(B) * cos(G) ± cos(A) * sin(B) ,
где
K - коэффициент мощности,
A - угол падения рудного тела,
B - вертикальный угол интервала,
G - острый угол между азимутом падения рудного тела и азимутом интервала.
В результате получается столбец с коэффициентом приведения к истинной мощности, который далее можно использовать при формировании рудных интервалов.
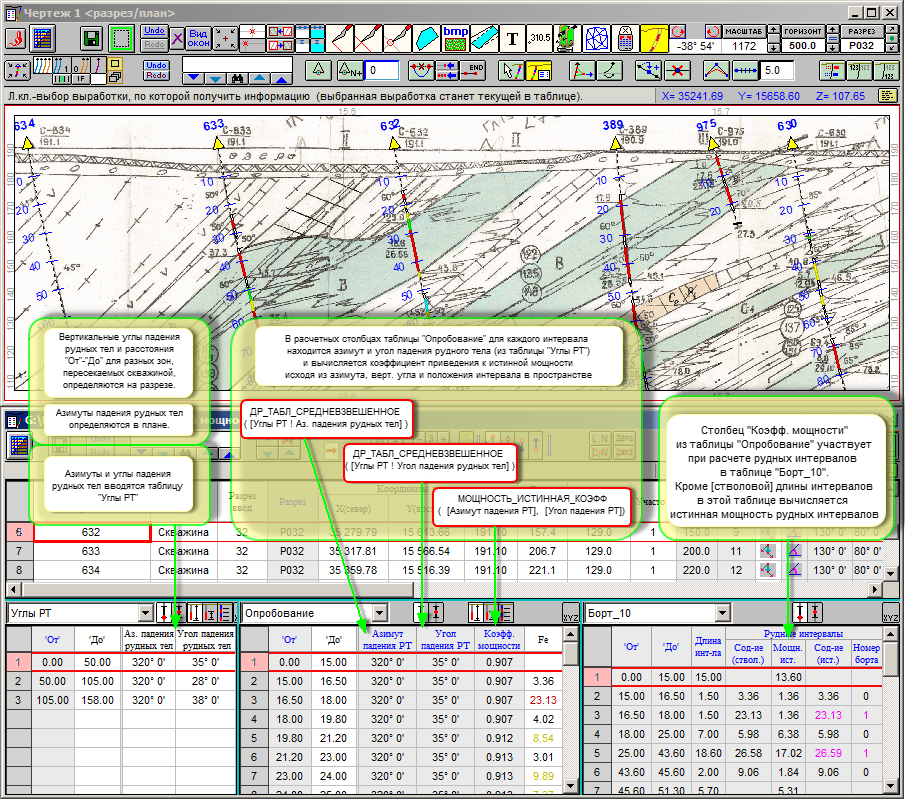
На приводимом ниже рисунке показан пример использования вспомогательной таблицы "Углы РТ", используемой для вычисления коэффицента приведения к истинной мощности для каждого интервала в таблице "Опробование" и последующим использованием полученных коэффициентов при расчете рудных интервалов (в таблице "Борт_10") :
Корректировка значения вертикального угла, измеренного на разрезе
В том случае, если линия разреза, на котором производится измерение вертикальных углов, не совпадает с направлением падения рудного тела (т.е. разрез не строго вкрест простирания), измеренный вертикальный угол будет отличаться от истинного вертикального угла.
Истинный вертикальный угол рудного тела всегда будет меньше или равен углу, измеренному на разрезе.
Величину истинного вертикального угла можно вычислить по формуле:
A = arctg ( tg ( As ) * cos ( U ) ),
где
As - вертикальный угол, измеренный на разрезе
U - угол между азимутом линии разреза и азимутом линии падения рудного тела.
Корректировку вертикального угла можно произвести либо в расчетном столбце, либо вместо функцииМОЩНОСТЬ_ИСТИННАЯ_КОЭФФ использовать функцию МОЩНОСТЬ_ИСТИННАЯ_КОЭФФ_УГОЛ_С РАЗРЕЗА, в которой третьим параметром является азимут линии разреза.
Во втором случае корректировка вертикального угла падения рудного тела производится внутри функции в процессе вычисления коэффициента приведения к истинной мощности и не требуется выполнять какие-либо дополнительные действия.
Иллюстрация к формуле П.М.Леонтовского
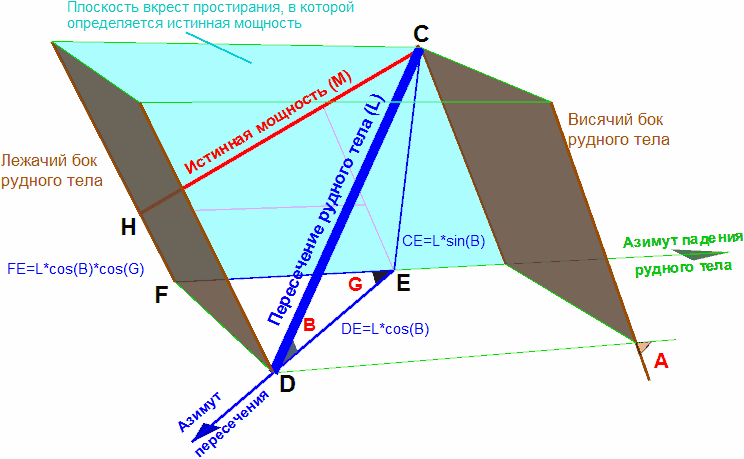
Исходные данные:
A - угол падения рудного тела
B - угол падения пересечения (или прямолинейного интервала по скважине)
Азимут падения рудного тела
Азимут пересечения.
L - длина пересечения
Вычисляется G - [острый] угол между заданными азимутами (азимутом падения рудного тела и азимутом пересечения).
Из прямоугольного треугольника CDE находятся:
- проекция пересечения на вертикальную плоскость CE = L * sin ( B)
- проекция пересечения на горизонтальную плоскость DE = L * cos ( B)
- проекция отрезка DE на расчетную плоскость, в которой определяется истинная мощность FE = DE * cos(G) = L * cos(B) * cos(G)
Далее рассматривается плоская задача (в расчетной плоскости, проведенной вкрест простирания):
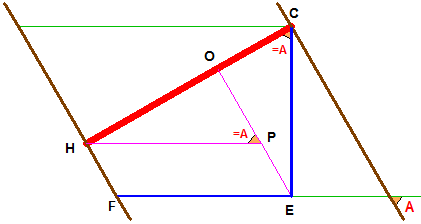
Известны CE и FE, необходимо найти истинную мощность CH.
Опустим из точки E перпендикуляр EO на отрезок CH (этот перпендикуляр будет параллелен линии падения рудного тела).
Найдем отрезки HО и ОС, из которых состоит искомый отрезок истинной мощности CH.
В треугольнике OHP сторона HP параллельна и равна FE, а угол OPH равен углу A.
Следовательно HO = HP * sin ( A ) = FE * sin ( A ) = L * cos(B) * cos(G) * sin ( A )
Угол ОСЕ равен углу падения рудного тела A (взаимно перпендикулярные стороны).
OC = CE * cos ( A ) = L * sin ( B ) * cos ( A )
Таким образом, истинная мощность равна:
CH = HO + OC = L * cos(B) * cos(G) * sin ( A ) + L * sin ( B ) * cos ( A ) = L * ( cos(B) * sin ( A ) * cos(G) + sin ( B ) * cos ( A ) )
Рассмотренная конфигурация треугольников получается в случае, когда азимут пересечения и азимут падения рудного тела направлены в разные стороны.
Для случая, когда когда азимут пересечения и азимут падения рудного тела направлены в одну сторону, в формуле используется знак "минус" (в двух вариантах):
CH = L * ( cos(B) * sin (A) * cos(G) - sin(B) * cos(A) )
CH = L * ( sin(B) * cos (A) - cos(B) * sin(A) * cos(G) )
Для пересечений (интервалов), имеющих направление снизу вверх, т.е. имеющих вертикальный угол с минусом, правила использования знаков "плюс" или "минус" в формуле меняются на противоположные. Подразумевается, что угол падения рудного тела всегда с плюсом.