Построение модели поверхности в виде сферы, описанной вокруг четырех точек (тетраэдра).
Построение модели поверхности в виде сферы, описанной вокруг четырех точек (тетраэдра).
|
<< Click to Display Table of Contents >> Navigation: РЕЖИМЫ РАБОТЫ В ОКНАХ-ЧЕРТЕЖАХ > < Работа с триангулированными моделями поверхностей >
|
В этом режиме производится построение модели поверхности в виде сферы, описанной вокруг тетраэдра, задаваемого четырьмя точками или треугольником и точкой.
Полученная сфера добавляется в новую модель поверхности текущего основного файла с моделями поверхностей.
Получаемая замкнутая модель поверхности-сфера будет состоять из треугольников, то есть будет некоторым приближением истинной сферы. Поэтому исходные четыре точки не будут абсолютно точно попадать в плоскости треугольников модели поверхности. Степень соответствия модели поверхности истинной сфере зависит от количества треугольников, из которых состоит сфера.
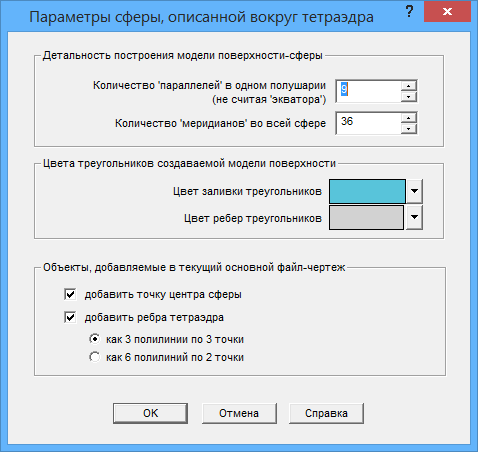
Параметры сферы (детальность построения модели поверхности, цветовые настройки) задаются в диалоге "Параметры сферы, описанной вокруг тетраэдра", вызываемом при нажатии на в любом месте графического окна.
В этом же диалоге определяется, нужно ли записывать в текущий основной файл-чертеж точку центра сферы и ребра тетраэдра, получаемого из заданных 4-х точек.
Четыре точки, являющиеся вершинами тетраэдра, вокруг которого строится описанная сфера, задаются либо поодиночке, либо сначала выбирается треугольник какой-либо модели поверхности (т.е. за один прием задаются первые три точки), после чего задается четвертая вершина тетраэдра.
- выбор точки тетраэдра (первой, второй, третьей или четвертой) среди существующих точек каких-либо объектов (точек, точек полилиний, точек моделей поверхностей, маркшейдерских отметок и т.п.).
Если рядим с курсором будет попадание в какой-либо объект, но не точно в точку (например, между точками полилинии или на ребро треугольника), то будет задан вопрос:
В случае положительного ответа точка будет использована при дальнейших построениях.
- в качестве точки тетраэдра (первой, второй, третьей или четвертой) будет использована точка мягкой стыковки к любому из объектов.
- выбор треугольника модели поверхности, три точки этого треугольника будут первыми тремя точками тетраэдра. Четвертая точка выбирается одним из способов, описанных выше.
Каждая из выбранных точек отмечается соответствующим маркером.
После выбора четвертой точки программа производит построение модели поверхности-сферы и выводит ее в графическое окно (фиолетовым цветом).
Далее:
- подтверждение построения модели поверхности-сферы и запись ее в текущий основной файл с моделями поверхностей.
- отмена построения модели поверхности-сферы.
Построение модели поверхности сферы по трем точкам
Если после ввода первых трех точек (или треугольника) нажать , то будет построена модель поверхности-сфера по трем точкам.
Центр такой сферы будет лежать в плоскости, проходящей через указанные три точки.
Пример построения модели поверхности-сферы
- выбор треугольника модели поверхности, три точки этого треугольника будут первыми тремя точками тетраэдра:
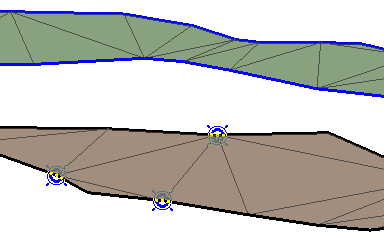
- выбор четвертой точки тетраэдра на противоположной модели поверхности, после чего сразу производится построение сферы:
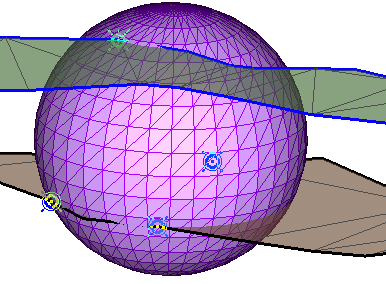
В окне с информацией о работе программы выводится информация о координатах точки центра сферы и радиусе сферы:
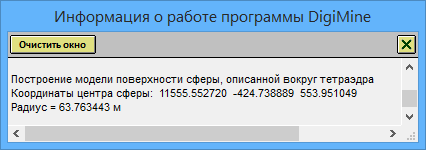
- подтверждение построения модели поверхности-сферы и запись ее в текущий основной файл с моделями поверхностей:
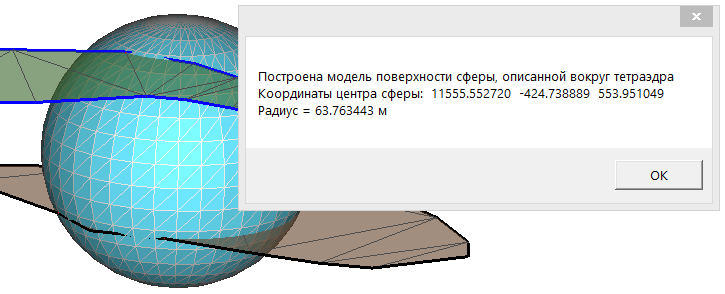
В окне с информацией о работе программы выводится информация о координатах точек тетраэдра и объектах, добавленных в основной файл-чертеж (если такие имеются):
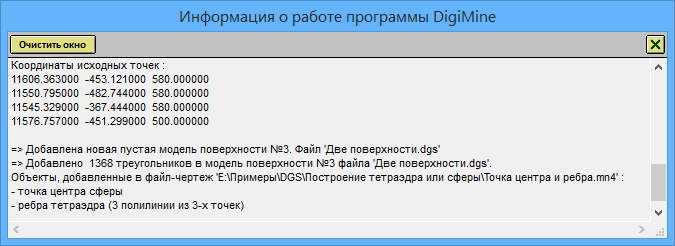
То же самое, но включена прозрачность модели поверхности-сферы и выключена отрисовка ее ребер (видны ребра тетраэдра и точка центра сферы):
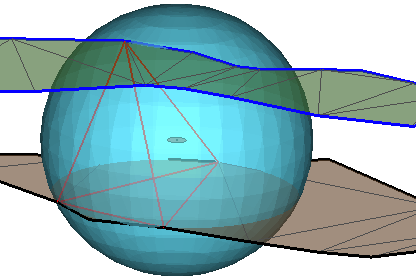
При записи полилиний-ребер тетраэдра используются параметры (стиль, толщина, цвет и т.п.), заданные для текущей полилинии в том окне, в котором производится построение, а при записи точки центра сферы - параметры текущей точки.
В диалоге "Параметры сферы, описанной вокруг тетраэдра" была задана запись в файл-чертеж точки центра сферы и ребер тетраэдра, вокруг которого строится описанная сфера:
