Триангуляция Делоне
В триангуляции Делоне в качестве исходных данных используются только точки.
(Вопрос о том, почему для построения поверхностей чаще всего используется именно триангуляция Делоне, здесь не рассматривается, на эту тему есть большое количество соответствующей литературы.).
Все треугольники триангуляции Делоне удовлетворяют условию Делоне: внутрь окружности, описанной вокруг треугольника, не попадает ни одна из точек, участвующих в триангуляции.
На приводимом рисунке показаны описанные окружности для нескольких треугольников триангуляции Делоне:
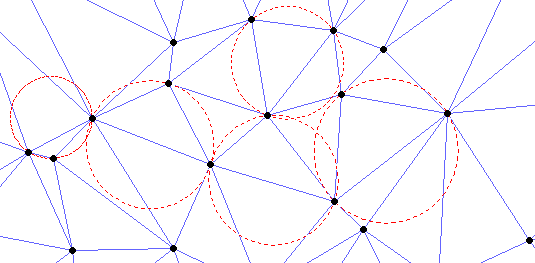
Заметим, что одним из свойств триангуляции Делоне является максимизация минимального угла среди всех углов всех построенных треугольников, т.е. можно говорить о минимизации количества треугольников с острыми углами.
Триангуляция Делоне с ограничениями
При построении моделей поверхностей, во многих случаях в качестве исходных данных используются не только точки, но и полилинии.
То есть некоторые ребра будущих треугольников присутствуют уже в исходных данных, причем новые ребра, получаемые в результате триангуляции, не должны пересекать ребра, полученные из полилиний.
Триангуляция с использованием не только точек, но и полилиний называется триангуляцией Делоне с ограничениями.
При триангуляции Делоне с ограничениями в создании нового треугольника не могут принимать участия точки, соединение с которыми приводит к получению ребер, пересекающих ребра, полученные из исходных полилиний. Для точек, которые могут принимать участие в образовании нового треугольника, действует то же правило (условие Делоне), как и в триангуляции без ограничений.
На следующем рисунке показано, что для точек 1, 2, 3, 4 условию Делоне удовлетворяет треугольник, составленный из точек 1, 2, 4 (и смежный с ним треугольник из точек 2, 3, 4).
Однако построен треугольник из точек 1, 3, 4 и треугольник из точек 1, 2, 3, потому что ребро из точек 1 и 3 получено из исходной полилинии. Если построить треугольник 1-2-4, то получится ребро 2-4, которое будет пересекать исходное ребро 1-3, что недопустимо:
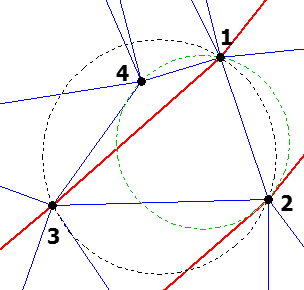
Недостатки триангуляции Делоне с ограничениями
Из-за того, что часть ребер подаются на вход триангуляции в готовом виде, возможно появление треугольников с более острыми углами, чем в том случае, если бы на вход триангуляции подавался тот же набор точек, но без заранее соединенных ребер. Однако этот недостаток не очень существенен, тем более что в определенной степени с ним можно бороться, если в исходных полилиниях не допускать "больших" расстояний между точками.
У триангуляции Делоне с ограничениями имеется гораздо более серьезный недостаток, который рассмотрим ниже.
На приводимом ниже рисунке показан фрагмент модели поверхности, полученный в результате триангуляции Делоне с ограничениями. В качестве исходных данных использованы изолинии рельефа:
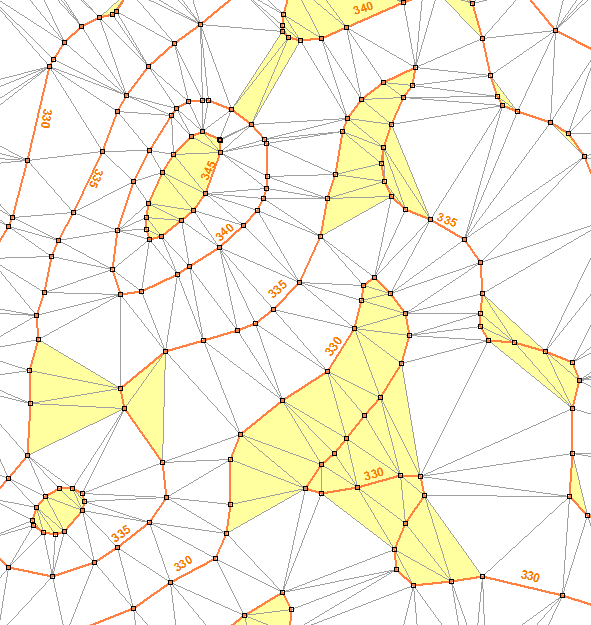
Отметим, что в результате триангуляции получено некоторое количество горизонтальных треугольников, которые опираются на точки одной и той же изолинии, либо на точки разных изолиний с одинаковой высотной отметкой. Горизонтальные площадки, составленные из таких треугольников, на рисунке закрашены желтым цветом.
На следующем рисунке – фрагмент того же участка модели поверхности в 3D окне:

С уверенностью можно сказать, что истинная поверхность не имеет таких горизонтальных площадок, которые получены в результате триангуляции.
Теоретически, конечно, могут быть единичные горизонтальные треугольники, но это исключение, а не правило.
Таким образом, если в чистом виде использовать триангуляцию Делоне с ограничениями применительно к изолиниям рельефа, то:
1. Модель поверхности будет содержать заведомые ошибки в случае использования ее для подсчета объемов.
2. Визуально модель поверхности будет выглядеть неестественно.
"Рисунок" изолиний – дополнительный источник информации
Форма изолиний рельефа и их взаимное расположение несут дополнительную информацию о характере поверхности. Анализируя изолинии человек в состоянии распознать, где примерно проходят тальвеги и водоразделы, где получаются седловины.
Конечно, невозможно абсолютно точно сказать, как ведет себя поверхность в каждой конкретной точке. Однако использование общих закономерностей характера поверхности в зависимости от формы и расположения изолиний позволяет существенно приблизить модель поверхности к описанию истинной поверхности.
Можно вручную достроить некоторые элементы рельефа. Наиболее очевидными элементами, которые могут улучшить модель поверхности, являются тальвеги. Несколько труднее выделять водоразделы.
Кстати, в программе DIGIMINE имеются удобные механизмы для выполнения задачи типа построения тальвегов, вручную. Если в процессе ввода тальвега сначала пристыковаться к одной изолинии, ввести промежуточные точки, а потом пристыковаться к другой изолинии, то промежуточным точкам вводимой полилинии будут автоматически присвоены "правильные" высотные отметки.
Однако улучшение модели поверхности путем достраивания элементов рельефа вручную, является очень трудоемкой задачей, так как количество горизонтальных площадок, получаемых в результате триангуляции Делоне с ограничениями, зачастую измеряется сотнями и даже тысячами. Кроме того, в ряде случаев, особенно при разветвлении линий водоразделов, непросто определить положение и отметки достраиваемых элементов рельефа.
Проблемы триангуляции - не только с изолиниями
Выше были рассмотрены проблемы, возникающие при построении моделей поверхностей с использованием изолиний.
Однако в построении моделей поверхностей часто используются полилинии, описывающие состояние горных работ – верхние и нижние бровки уступов/отвалов, линии разделения уступов.
Для них также возможно возникновение проблем, сходных с теми, которые имеют место для изолиний рельефа.
Например, появление площадки между отвалами (при правильном построении должен быть построен некий аналог тальвега):
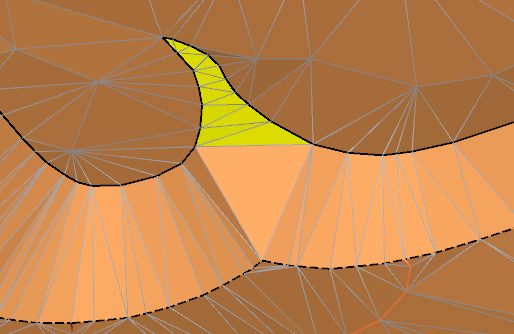
Некорректные площадки появляются также при триангуляции откосов уступов:
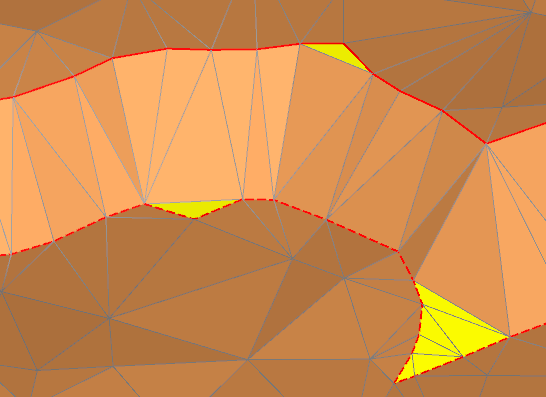
В случае с уступами и отвалами получаемые площадки, в общем случае, не являются горизонтальными, что несколько осложняет их распознавание (по сравнению с изолиниями).
Отметим, что для площадок (берм) между уступами применение дополнительных построений не является очевидным. В общем случае высотные отметки на таких площадках (бермах) носят случайный характер, поэтому для них целесообразно производить лишь триангуляцию Делоне с ограничениями, а дополнительные построения делать только для откосов уступов/отвалов.
В некоторых программах используются алгоритмы, которые стараются решить проблемы, возникающие при триангуляции Делоне с ограничениями, следующим образом: по возможности не соединяют между собой точки, принадлежащие одной изолинии или разным изолиниям с одинаковыми отметками, а отдают предпочтение соединению между собой точек, принадлежащих разным полилиниям (соединение в пределах прямой видимости). Но такое возможно не всегда, а только в тех случаях, когда получаемое в результате ребро не пересекает существующие ребра (полученные из отрезков исходных полилиний). Кроме того, для этих алгоритмов характерно появление треугольников, которые, во-первых, имеют очень острые углы и, во-вторых, очень круто наклонены к горизонтальной плоскости.
В программе DIGIMINE реализовано несколько вариантов триангуляции. Кроме триангуляции Делоне с ограничениями и упомянутой триангуляции с соединением в пределах прямой видимости, имеются еще 2 варианта триангуляции, в которых строятся треугольники, описывающие выпуклые или вогнутые формы рельефа (тальвеги/водоразделы, седловины, вершины/впадины). Более подробно – см. Варианты триангуляции при построении модели поверхности в программе DIGIMINE.