При построении каркасов в программе довольно часто используется вычисление 'усредненной' плоскости для исходных замкнутых контуров.
Это связано с тем, что точки исходных контуров часто не лежат в одной плоскости, а для некоторых алгоритмов в процессе расчетов необходимо привести исходный контур к плоскому виду, спроецировав его на 'усредненную' плоскость.
Например, в режиме "'Выдавливание' полилиний" можно задать, чтобы новая полилиния смещалась в направлении нормали к плоскости исходного контура. Т.к. для построения нормали необходима плоскость, программа предварительно вычисляет 'усредненную' плоскость.
В режиме "Соединение двух полилиний" при операциях с замкнутыми исходными контурами программа также производит (в неявном для пользователя виде) вычисление 'усредненных' плоскостей и использует их при построениях триангуляции.
Вычисление 'усредненной' плоскости производится и в ряде других режимов, используемых при построении каркасов.
Что же такое 'усредненная' плоскость и каковы особенности работы с ней ?
Уравнение 'усредненной' плоскости рассчитывается по минимуму суммы квадратов расстояний точек исходной полилинии до этой плоскости.
Если все точки исходной полилинии лежат в одной плоскости (например, в плоскости разреза), то 'усредненная' плоскость будет совпадать с этой плоскостью.
Иллюстрация проекции полилинии на 'усредненную' плоскость:
Исходная полилиния:
Исходная полилиния и ее проекция на 'усредненную' плоскость (в виде закрашенного плоского полигона):

То же, под другим углом зрения:
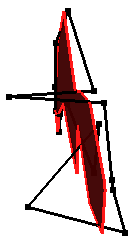
Усредненная плоскость для линейно вытянутых контуров
В некоторых случаях 'усредненная' плоскость, которая рассчитывается по минимуму суммы квадратов расстояний, может оказаться в таком положении, которое отличается от ожиданий пользователя.
Иногда может получиться такая 'усредненная' плоскость, при проецировании на которую получается контур, имеющий пересечения отрезков между собой.
Например:
То же, под другими углами зрения (и в другом масштабе):
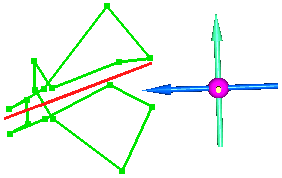
В приведенном примере исходный (зеленый) контур формировался на вертикальном разрезе, поэтому пользователь может ожидать, что 'усредненная' плоскость будет близка к вертикальной плоскости.
Однако расчет по минимуму суммы квадратов расстояний дает такую плоскость, которая ближе к горизонтальной плоскости, чем к вертикальной.
На рисунках мы видим, что исходный контур является линейно вытянутым в направлении примерно запад-восток (оранжевая стрелка). Точки, располагающиеся друг напротив друга по вертикали имеют относительно небольшое расстояние между собой - по сравнению с расстоянием между соседними точками в направлении юг-север (синяя стрелка). Поэтому расчет по минимуму квадратов расстояний и дает плоскость, проходящую между верхними и нижними точками исходного контура. Математически все правильно, но для использования при построении каркасов такая 'усредненная' плоскость явно не подходит.
Особенности работы с линейно вытянутыми контурами
В программе DIGIMINE предусмотрены механизмы, позволяющие разрешать проблемы 'усредненной' плоскости при работе с линейно вытянутыми контурами.
Заметим, что для более удобной работы с линейно вытянутыми контурами имеется возможность укрупнять масштаб изображения в том направлении, в котором контур является узким.
В рассмотренном выше примере будет удобным сделать более крупным масштаб изображения по оси Z:
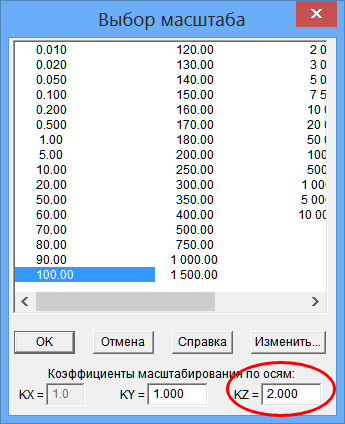
При вычислении 'усредненной' плоскости DIGIMINE учитывает коэффициенты растяжения/сжатия масштаба изображения по осям.
(В остальных случаях при расчетах используются истинные координаты точек объектов, а коэффициенты сжатия/растяжения по осям влияют только на отображение объектов в окне).
Автоматическое использование коэффициентов изменения масштаба изображения по осям обусловлено тем, что при работе с линейно вытянутыми контурами масштабирование по осям делает построение каркасов более удобным и, как правило, используется в работе.
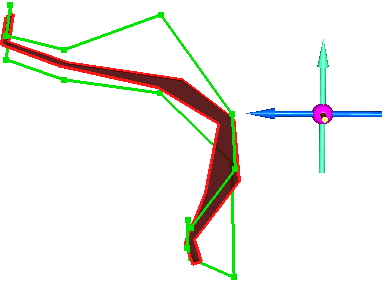
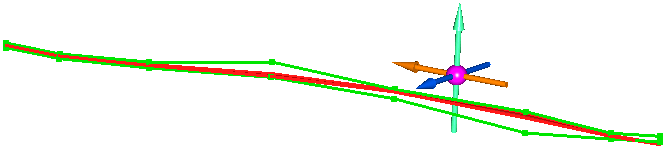
Рассмотрим, как изменится положение 'усредненной' плоскости для рассмотренного выше контура в случае использования коэффициента KZ=2.0, укрупняющего масштаб изображения по оси Z в 2 раза.
На трех рисунках, под разными углами зрения, показаны исходный контур (зеленого цвета), проекция исходного полигона на 'усредненную' плоскость, отстроенная в предыдущем примере, с KZ=1.0 (красного цвета) и проекция исходного полигона на 'усредненную' плоскость, отстроенная с KZ=2.0 (синего цвета):
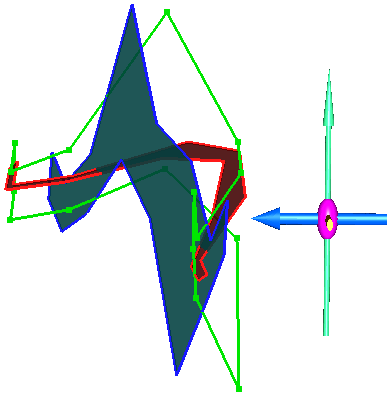
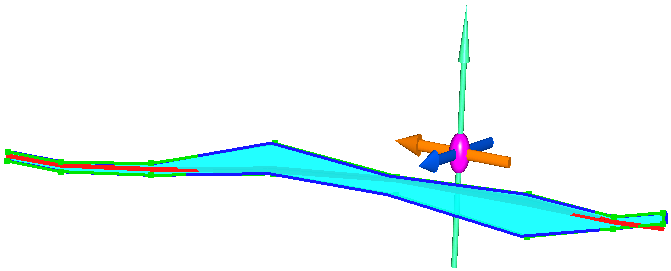
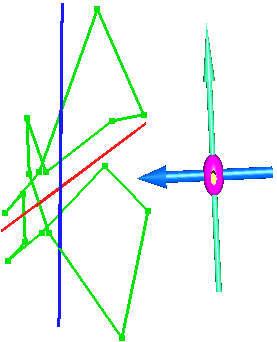
Как можно видеть на последних трех рисунках, 'усредненная' плоскость стала близка к вертикальной, что и требовалось для нормальной работы при построении каркасов.
В данном случае укрупнение изображения все лишь в 2 раза привело к желаемому результату.
На практике, при работе с линейно вытянутыми контурами нередко используются и большие значения коэффициентов, изменяющих масштаб изображения по осям.
РЕКОМЕНДУЕТСЯ ПРИ ПОСТРОЕНИИ КАРКАСОВ ПО ЛИНЕЙНО ВЫТЯНУТЫМ КОНТУРАМ ИСПОЛЬЗОВАТЬ ИЗМЕНЕНИЕ МАСШТАБА ИЗОБРАЖЕНИЯ ПО ОСЯМ