Периодически приходится иметь дело с замкнутыми моделями поверхностей ('каркасами'), которые являются составными частями некоторого объекта большего размера. Например, одно рудное тело может иметь окисленную и сульфидную части.
Для корректной работы с такими объектами необходимо обеспечивать 'плотное ' прилегание смежных модели поверхностей друг к другу.
В DIGIMINE реализованы механизмы, позволяющие отслеживать 'плотное' прилегание моделей поверхностей и автоматически обеспечивать построение одинаковых треугольников, располагающихся между моделями поверхностей. Включение/выключение этих механизмов производится в диалоге "Параметры триангуляции между двумя полилиниями", причем можно отслеживать либо только те поверхности, которые имеются в текущем основном файле с моделями поверхностей, либо все поверхности во всех загруженных файлах с моделями поверхностей.
Отслеживание 'плотного' прилегания моделей поверхностей может использоваться при работе в режимах ![]() ,
, ![]() и
и ![]() .
.
Принцип работы с 'плотными' прилеганиями следующий. Если в какой-либо из существующих моделей поверхностей (имеющихся в текущем основном файле с моделями поверхностей или во всех файлах, в зависимости от настроек), будут обнаружены треугольники, которые опираются на точки исходных полилиний, заданных для триангуляции, программа обеспечит запись идентичных треугольников в создаваемую модель поверхности.
Треугольники, все три точки которых принадлежат одной исходной полилинии, для данной задачи не используются.
Новая модель поверхности может прилегать к нескольким существующим моделям поверхностей.
Если заданы соединительные линии, которые попадают на найденные треугольники, общие для смежных моделей поверхностей, то такие соединительные линии программой отбраковываются и не принимают участия в расчетах. То есть 'плотное' прилегание имеет больший приоритет, чем соединительные линии.
Пример создания модели поверхности, смежной с другой моделью поверхности
На что обращать внимание в модели поверхности, к которой планируется 'плотное' прилегание
При построении моделей поверхностей следует обращать внимание на построения треугольников в той модели поверхности, к которой будет прилегать другая поверхность.
Главное правило - концы линий, разделяющих две смежные модели поверхности должны соединяться между собой ребрами треугольников:
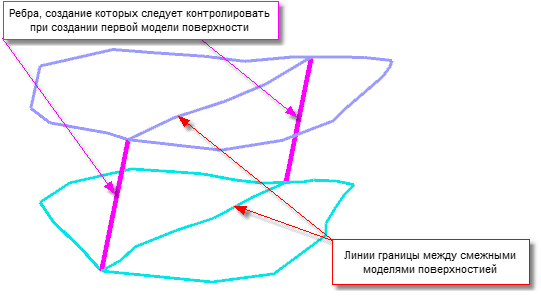
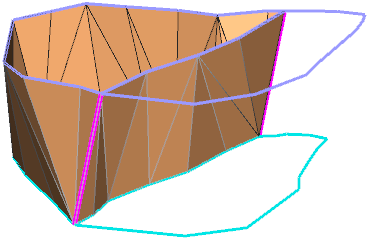
Правильное построение первой модели поверхности:
"Неправильное" построение первой модели поверхности:
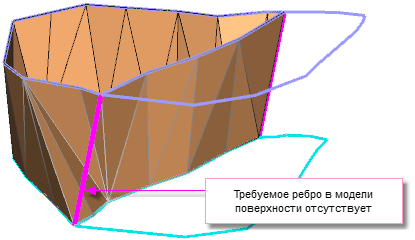
Теперь рассмотрим результат построения второй модели поверхности в первом и во втором случае. Треугольники первой модели поверхности показаны с заливкой, но без ребер, для треугольников второй модели поверхности, наоборот, показаны ребра, но нет заливки.
Правильное построение первой модели поверхности:
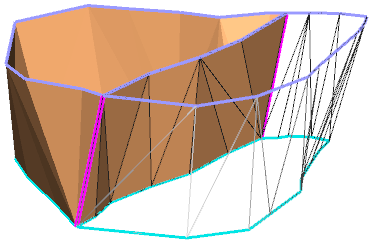
"Неправильное" построение первой модели поверхности:
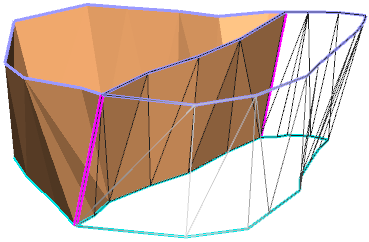
В этом случае не для всех треугольников, опирающихся на линии, разделяющие две поверхности возможно 'плотное' прилегание, хотя чисто геометрической ошибки здесь нет (поэтому слово "Неправильное" взято в кавычки). В принципе, пользователь мог и сознательно выполнить подобное построение.
Однако если в "неправильной" области к этим двум поверхностям будет прилегать некоторая третья модель поверхности, в построении которой будут принимать те же исходные полилинии, то на стыке трех моделей поверхностей образуется небольшая "дырка".
Поэтому следует контролировать правильность построения моделей поверхностей принимая во внимание описанные выше замечания, тем более, что это не представляет особой сложности, только не стоит забывать об этом.
Следует также обратить внимание на тот факт, что подобного рода "неправильные" построения более вероятны при использовании алгоритма минимизации площади и гораздо менее вероятны при использовании других алгоритмов, которые достаточно хорошо работают в местах "перегибов" полилиний, используемых при триангуляции. Поэтому, при использовании алгоритма минимизации площади придется чаще использовать соединительные линии.