Во многих случаях алгоритмы триангуляции между двумя полилиниями в пространстве, основанные на таких критериях, как минимальная суммарная площадь треугольников, получение треугольников с углами, не сильно отличающимися друг от друга и т.п. приводят к таким построениям, которые выглядят нелогично с точки зрения правильности перехода от одной полилинии к другой.
Вряд ли возможен такой алгоритм триангуляции между двумя полилиниями в пространстве, который бы абсолютно всегда приводил к результату, удовлетворяющему пользователя. Тем более - при построении каркасных моделей рудных тел, когда на оценку правильности полученного результата могут оказывать влияние не только геометрические характеристики полилиний, непосредственно участвующих в триангуляции, но и некоторые характеристики рудного тела в целом. Однако необходимо стремиться к созданию таких алгоритмов, которые бы минимизировали количество ситуаций, требующих ручного вмешательства.
В DIGIMINE реализованы 3 алгоритма триангуляции:
- минимизации суммарной площади получаемых треугольников;
- поиска подобия исходных полилиний;
- комбинированный алгоритм, использующий критерии обоих вышеуказанных алгоритмов и позволяющий при помощи некоторого целочисленного параметра задавать "степень участия" одного или другого.
Алгоритму минимизации площади присвоен индекс 0, алгоритму поиска подобия исходных полилиний - индекс 10, а для комбинированного алгоритма используются индексы от 1 до 9, причем увеличение индекса комбинированного алгоритма говорит об увеличении в нем роли алгоритма поиска подобия исходных полилиний и снижении роли алгоритма минимизации площади.
Эти индексы, в частности, используются для отображения текущего алгоритма триангуляции в графическом меню.
Описываемые здесь алгоритмы триангуляции используются при работе в режимах ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
Особенности триангуляции при использовании разных алгоритмов
У алгоритма минимизации площади имеется очень существенный недостаток при триангуляции на "перегибах" исходных полилиний - соединение точек, которые находятся по одну сторону от "перегиба" на одной полилинии с точками, которые находятся по другую сторону от "перегиба" на другой полилинии, т.е. этот алгоритм совершенно не "чувствует" форму исходных полилиний.
Алгоритм поиска подобия исходных полилиний, напротив, весьма неплохо "чувствует" форму исходных полилиний и, в подавляющем большинстве случаев, уверенно находит характерные точки (и фрагменты) "перегибов". Однако при использовании этого алгоритма возможно появления большего количества "вееров" треугольников. Впрочем, при детальном рассмотрении, во многих случаях появление "вееров" треугольников вполне логично.
Комбинированный алгоритм на "перегибах" работает ближе к алгоритму поиска подобия, даже при небольших значениях индекса этого алгоритма. На относительно плавных участках результат его работы в большей степени зависит от значения индекса.
Отметим, что результат триангуляции для комбинированного алгоритма при изменении индекса на 1 часто меняется очень незначительно. Однако, в некоторых случаях, изменение индекса комбинированного алгоритма на 1 приводит к довольно-таки существенному изменению в получаемой триангуляции. Причем этот "скачок" может оказаться как среди индексов с небольшими значениями, так и среди индексов с большими значениями. Именно этим и обусловлено достаточно большое количество индексов (от 1 до 9) комбинированного алгоритма.
Однозначный ответ на вопрос о том, какой из имеющихся алгоритмов является лучшим, дать затруднительно.
Но достаточно уверенно можно рекомендовать пореже использовать алгоритм с минимизацией площади, а если использовать - то обращать особое внимание на места "перегибов" исходных полилиний и исправлять триангуляцию в проблемных местах при помощи соединительных линий.
Отметим, что алгоритм поиска подобия и комбинированный алгоритм, как правило, создают гораздо меньше случаев, требующих вмешательства человека. Если исходные контуры глобально являются более или менее подобными, то применение алгоритмов поиска подобия исходных полилиний или комбинированного алгоритма достаточно часто не требует никаких дополнительных корректировок.
Совмещение центров масс исходных замкнутых полилиний (в процессе расчетов)
Для замкнутых полилиний перед проведением триангуляции в большинстве случаев желательно чтобы программа предварительно выполняла [внутреннюю] операцию нахождения центров масс проекций полилиний на усредненную плоскость и совмещение центров масс исходных полилиний. Использование этой операции задается в диалоге "Параметры триангуляции между двумя полилиниями".
Когда две исходные полилинии, между которыми производится триангуляция находятся не "в створе" друг относительно друга, возникают побочные эффекты, приводящие в ряде случаев к некорректной триангуляции. В основном это касается алгоритма минимизации площади, в меньшей степени затрагивает комбинированный алгоритм и не влияет на алгоритм поиска подобия.
Выполнение совмещения центров масс проекций исходных полилиний позволяет в большинстве случаев улучшить качество триангуляции, т.е. получить более логичные соединения точек исходных полилиний между собой.
Однако следует обратить внимание на тот факт, что при использовании такого совмещения для алгоритма минимизации площади (а именно для него, в первую очередь и предназначена рассматриваемая опция) можно получить суммарную площадь треугольников, не являющуюся минимальной. В процессе расчетов, для смещенных полилиний, площадь на самом деле будет минимальной, но для итоговой модели поверхности, с несмещенными точками, площадь может и не быть минимальной.
Информация о площади треугольников и объеме (для замкнутых)
Для треугольников, построенных при триангуляции вычисляется суммарная площадь.
Если в триангуляции принимают участие замкнутые полилинии, то производится триангуляция внутри этих полилиний (во вспомогательной рабочей модели поверхности, не являющейся выходной) и вычисляется [потенциальный] объем в полученной замкнутой модели поверхности.
Заметим, что суммарная площадь треугольников и [потенциальный] объем напрямую не связаны между собой. При увеличении площади объем может как увеличиваться, так и уменьшаться.
Информация о текущем алгоритме триангуляции, суммарной площади и [потенциальном] объеме модели поверхности (для замкнутых полилиний) выводится в окно с информацией о работе программы, что позволяет сравнивать эти показатели для моделей поверхности, построенных по разным алгоритмам:

Необходимо учитывать (см. выше о совмещении центров масс), что для алгоритма минимизации площади фактическая площадь треугольников может оказаться больше, чем площадь треугольников, полученных по другим алгоритмам.
Изменение алгоритма триангуляции
Текущий алгоритм триангуляции между полилиниями может быть изменен либо в диалоге "Параметры триангуляции между двумя полилиниями", либо в графическом меню, где выводится индекс текущего алгоритма : ![]() .
.
Алгоритм триангуляции можно изменять не только до начала триангуляции, но и в процессе работы по триангуляции между полилиниями. Если в момент изменения алгоритма триангуляции в окне изображается [предварительно] построенная, но еще не подтвержденная триангуляция, происходит автоматический пересчет триангуляции с новым алгоритмом.
Пример изменения алгоритма триангуляции в процессе соединения полилиний
Возможные пересечения треугольников
При триангуляции между двумя полилиниями не исключается появление пересекающихся между собой треугольников, хотя программой предпринимаются некоторые меры для предотвращения этого.
Если в триангуляции, которая должна записываться в файл (после подтверждения), будут обнаружены пересекающиеся треугольники, то программа выдает сообщение об этом. Пользователь может отказаться от записи, чтобы произвести необходимые корректировки - изменить алгоритм триангуляции или добавить/удалить соединительные линии.
Если запись в файл все-таки производится, то пересекающиеся треугольники можно впоследствии выявить в процессе проверки моделей поверхностей.
Ниже приводится пример триангуляции между полилиниями, в которых пересекающиеся треугольники ликвидируются за счет изменения алгоритма триангуляции.
Для приведенного примера в окне с информацией о работе программы будет выведено следующее:
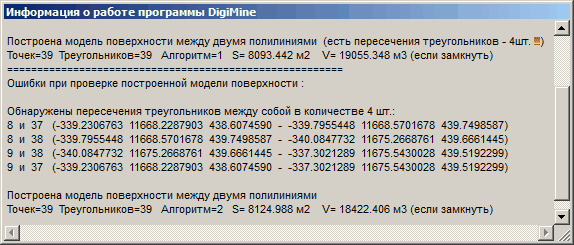
После построения по алгоритму 1 выведена информация о построенной поверхности, а также о том, что имеются пересечения треугольников в количестве 4 шт.
Далее, после того, как было первое подтверждение на запись (которое в примере привело к появлению предупреждения), выведена детальная информация о пересекающихся треугольниках и координатах отрезков пересечения треугольников.
Наконец, после перетриангуляции по алгоритму 2 выведена информация о построенной поверхности. Пересечений треугольников в этой поверхности не обнаружено.
Как можно видеть, сведения о наличии пересечений в триангуляции между полилиниями (если они есть) всегда выводятся в окно с информацией о работе программы, и, кроме того, появляется соответствующее предупреждение в случае, если перед записью модели поверхности в файл обнаружены пересечения треугольников.